题目内容
已知点P(6,8)是椭圆
+
=1(a>b>0)上一点,F1,F2为椭圆的两焦点,若
•
=0,试求:
(1)椭圆的方程.
(2)求sin∠PF1F2的值.
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
(1)椭圆的方程.
(2)求sin∠PF1F2的值.
分析:(1)利用数量积
•
=0,可得(-c-6)(c-6)+64=0,解得c.进而得到F1,F2,利用两点间的距离公式可得2a=|PF1|+|PF2|,再利用b2=a2-c2即可得出b2.
(2)如图所示,过点P作PM⊥x轴,垂足为M,则|PM|=8,|F1M|=10+6=16,利用勾股定理可得|PF1|,再利用sin∠PF1F2=
即可得出.
| PF1 |
| PF2 |
(2)如图所示,过点P作PM⊥x轴,垂足为M,则|PM|=8,|F1M|=10+6=16,利用勾股定理可得|PF1|,再利用sin∠PF1F2=
| |PM| |
| |PF1| |
解答:解:(1)∵
•
=0,
∴(-c-6)(c-6)+64=0,解得c=10.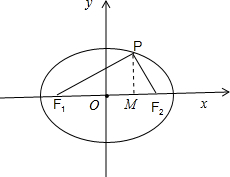
∴F1(-10,0),F2(10,0),
∴2a=|PF1|+|PF2|=
+
=12
,
∴a=6
,b2=80.
∴椭圆方程为
+
=1.
(2)如图所示,过点P作PM⊥x轴,垂足为M,则|PM|=8,|F1M|=10+6=16,
∴|PF1|=
=
=8
,
∴sin∠PF1F2=
=
=
.
| PF1 |
| PF2 |
∴(-c-6)(c-6)+64=0,解得c=10.

∴F1(-10,0),F2(10,0),
∴2a=|PF1|+|PF2|=
| (6+10)2+82 |
| (6-10)2+82 |
| 5 |
∴a=6
| 5 |
∴椭圆方程为
| x2 |
| 180 |
| y2 |
| 80 |
(2)如图所示,过点P作PM⊥x轴,垂足为M,则|PM|=8,|F1M|=10+6=16,
∴|PF1|=
| |PM|2+|F1M|2 |
| 162+82 |
| 5 |
∴sin∠PF1F2=
| |PM| |
| |PF1| |
| 8 | ||
8
|
| ||
| 5 |
点评:本题考查了向量垂直与数量积的关系、椭圆的定义域标准方程、勾股定理及其直角三角形的边角关系等基础知识与基本方法,属于基础题.

练习册系列答案
相关题目
已知点P在椭圆
+
=1上,F1,F2是椭圆的两个焦点,△F1PF2是直角三角形,则这样的点P有( )
| x2 |
| 40 |
| y2 |
| 20 |
| A、2个 | B、4个 | C、6个 | D、8个 |
已知点P(-4,8,6),则点P关于平面xoy对称的点的坐标是( )
| A、(-4,-8,6) | B、(-4,8,-6) | C、(4,-8,-6) | D、(4,-8,6) |