题目内容
已知点A(3,0)、B(0,3)、C(cosα,sinα),α∈(
).(1)若|
|=|
|,求角α的值;
(2)(理)若
=-1,求
的值.
(文)若(
)·
=2(O是坐标原点),求
的值.
解:(1)方法一:∵A(3,0)、B(0,3)、C(cosα,sinα),
∴=(cosα-3,sinα),=(cosα,sinα-3).
由||=||,得,
即cosα=sinα.
∵＜α＜,∴α=.
方法二:∵|
|=|
|,
∴点C在直线y=x上.
则sinα=cosα.
∵α∈(
),∴α=
.
(2)(理)
=2sinαcosα.
由
=-1,得
(cosα-3)cosα+sinα(sinα-3)=-1,
即sinα+cosα=
.
∴(sinα+cosα)2=1+2sinαcosα=
,
即2sinαcosα=
.
∴
.
(文)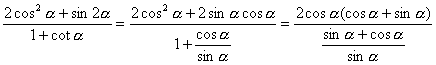
=2sinαcosα.
由(
)·
=2,
得sinα+cosα=
.
∴(sinα+cosα)2=1+2sinαcosα=
,
即2sinαcosα=
.
∴
.
上任意一点，∠AOP的平分线交PA于M(O为原点)，试求点M的轨迹.