题目内容
己知(b-c)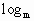 x+(c-a)
x+(c-a)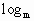 y+(a-b)
y+(a-b)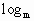 z=0,
z=0,
(1)设a,b,c依次成等差数列,且公差不为0,求证:x,y,z成等比数列;
(2)设正数x,y,z依次成等比数列,且公比不为1,求证:a,b,c成等差数列.
答案:
解析:
解析:
|
证 (1)∵a,b,c成等差数列,且公差d≠0,∴b-c=a-b=-d,c-a=2d.代入条件得-d( (2)∵x,y,z成等比数列且公比q≠1,∴y=xq,z= |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
己知函数f(x)=|x3+a|,a∈R在[-1,1]上的最大值为M(a),若函数g(x)=M(x)-|x2+t|有4个零点,则实数t的取值范围为.( )
A、(1,
| ||
| B、(-∞,-1) | ||
C、(-∞,-1)∪(1,
| ||
| D、(-∞,-1)∪(1,2) |
己知函数f(x)=|x3+a|,a∈R在[-1,1]上的最大值为M(a),则函数g(x)=M(x)-|x2-1|的零点个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
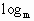 x-2
x-2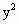 =xy,∵x,y,z均为正数,∴x,y,z成等比数列.
=xy,∵x,y,z均为正数,∴x,y,z成等比数列.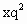 代入已知条件,得(b-c)
代入已知条件,得(b-c)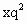 =0,∴(c+a-2b)
=0,∴(c+a-2b)