题目内容
已知虚数(x-2)+yi(x,y∈R)的模为| 3 |
| y |
| x |
| y+1 |
| x+1 |
分析:由题意求出x,y的关系,利用
的几何意义点与原点连线的斜率,求出它的最大值,类似求出
的最小值.
| y |
| x |
| y+1 |
| x+1 |
解答: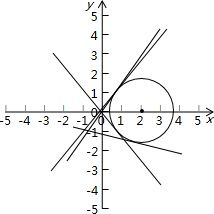 解:虚数(x-2)+yi(x,y∈R)的模为
解:虚数(x-2)+yi(x,y∈R)的模为
,即(x-2)2+y2=3
就是以(2,0)为圆心以
为半径的圆,
的几何意义点与原点连线的斜率,
易得
的最大值是:
的几何意义是圆上的点与(-1,-1)连线的斜率,求
的最小值
为:
=k,kx-y-1+k=0直线与圆相切时k最大和最小
=
解得k=
时最大.
故答案为:
;
.
 解:虚数(x-2)+yi(x,y∈R)的模为
解:虚数(x-2)+yi(x,y∈R)的模为| 3 |
就是以(2,0)为圆心以
| 3 |
| y |
| x |
易得
| y |
| x |
| 3 |
| y+1 |
| x+1 |
| y+1 |
| x+1 |
为:
| y+1 |
| x+1 |
| 3 |
| |2k-1+k| | ||
|
解得k=
3-
| ||
| 6 |
故答案为:
| 3 |
3-
| ||
| 6 |
点评:本题考查复数的基本概念,简单线性规划,复数求模,考查计算能力,是中档题.

练习册系列答案
相关题目
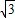 ,则
,则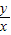 的最大值是 ,
的最大值是 ,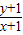 的最小值为 .
的最小值为 .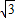 ,则
,则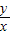 的最大值是 ,
的最大值是 ,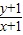 的最小值为 .
的最小值为 .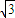 ,则
,则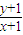 的最小值为 .
的最小值为 .