题目内容
如图,点A,B是单位圆上的两点,A,B点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(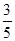 ,
,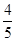 ),记∠COA=α.
),记∠COA=α.
(1)求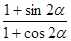 的值;
的值;
(2)求|BC|2的值.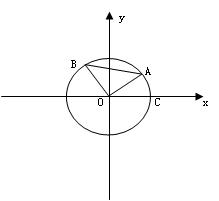
(1)∵A的坐标为(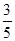 ,
,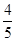 ),根据三角函数的定义可知,sinα=
),根据三角函数的定义可知,sinα=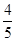 ,cosα=
,cosα=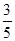 ,
,
∴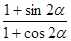 =
=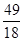 .……………7分
.……………7分
(2)∵△AOB为正三角形,∴∠AOB=60°.
∴cos∠COB=cos(α+60°)=cosαcos60°-sinαsin60°=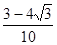 ,………11分
,………11分
∴|BC|2=|OC|2+|OB|2-2|OC|·|OB|cos∠COB=1+1-2×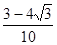 =
=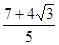 .
.
解析

练习册系列答案
相关题目
已知向量m= ,n=
,n= .
.
(1)若m·n=1,求cos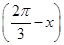 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
根据下列条件解三角形,两解的是( )
| A.b = 10,A = 45°,B = 70° |
| B.a = 60,c = 48,B = 100° |
| C.a = 14,b = 16,A = 45° |
| D.a = 7,b = 5,A = 80° |
在△ABC中,a=4,b=4 ,角A=30°,则角B等于 ( ).
,角A=30°,则角B等于 ( ).
| A.30° | B.30°或150° | C.60° | D.60°或120° |
 ,
, ,
, .
. 
 的值;
的值; 的值.
的值. 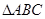 中,若
中,若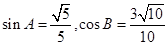 ,且
,且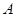 为锐角,求角
为锐角,求角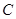 .
. 分)已知函数
分)已知函数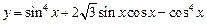 ,
,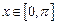 ,求该函数的单调递增区间。
,求该函数的单调递增区间。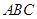 中,角
中,角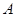 、
、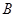 、
、 的对边分别为
的对边分别为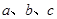 ,若
,若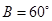 ,且
,且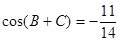 .
.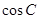 的值; (2)若
的值; (2)若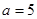 ,求△
,求△ ,
, ,求
,求 的值.
的值.