题目内容
设{an}是公差d不为零的正项等差数列,Sn为其前n项的和,满足5S3-6S5=-105,a2,a5,a14成等比数列.(1)求数列{an}的通项公式;
(2)设c∈N,c≥2,令bn=|
| an | 2c-1 |
分析:(1)根据等差数列求和公式分别表示出S3和S5,进而根据题设等式求得a1和d的关系式,用等差数列的通项公式表示出a2,a5,a14,根据等差数列等差中项的性质建立等式求得a1和d的另一关系式,进而联立求得a1和d的,则数列的通项公式可得.
(2)把(1)中求得的an代入求得bn,进而求得n≤c和n≥c+1时bn,进而利用等差数列和等比数列的求和公式求得前2c项的和,进而根据T2c≤6,求得c的范围,进而根据c∈N进而求得c的值.
(2)把(1)中求得的an代入求得bn,进而求得n≤c和n≥c+1时bn,进而利用等差数列和等比数列的求和公式求得前2c项的和,进而根据T2c≤6,求得c的范围,进而根据c∈N进而求得c的值.
解答:解:(1)∵Sn=na1+
,
∴S5=5a1+10d,S3=3a1+3d
∴5S3-6S5=-(15a1+45d)=-105
∴a1+3d=7①
又a2,a5,a14成等比数列.
∴(a5)2=a2a14,即(a1+4d)2=(a1+d)(a1+13d)
∴d2=2a1d,∵d≠0
∴d=2a1,②
由①②得a1=1,d=2
∴an=2n-1
(2)bn=|
-1|=|
|=
当n≤c时,bn=
,当n≥c+1时,bn=
∴Tn=b1+b2+…+b2c=(b1+b2+…+bc)+(bc+1+bc+2+…+b2c)=
=(
+
+…+
)+(
+
+…+
)=
∵Tn≤6,∴
≤6,
∴c2-6c+3≤0,解得3-
≤c≤3+
∵c∈N,
∴c=2或c=3或c=4或c=5.
| n(n-1)d |
| 2 |
∴S5=5a1+10d,S3=3a1+3d
∴5S3-6S5=-(15a1+45d)=-105
∴a1+3d=7①
又a2,a5,a14成等比数列.
∴(a5)2=a2a14,即(a1+4d)2=(a1+d)(a1+13d)
∴d2=2a1d,∵d≠0
∴d=2a1,②
由①②得a1=1,d=2
∴an=2n-1
(2)bn=|
| an |
| 2c-1 |
| 2(n-c) |
| 2c-1 |
| 2|n-c| |
| 2c-1 |
当n≤c时,bn=
| 2(c-n) |
| 2c-1 |
| 2(n-c) |
| 2c-1 |
∴Tn=b1+b2+…+b2c=(b1+b2+…+bc)+(bc+1+bc+2+…+b2c)=
=(
| 2(c-1) |
| 2c-1 |
| 2(c-2) |
| 2c-1 |
| 0 |
| 2c-1 |
| 2 |
| 2c-1 |
| 4 |
| 2c-1 |
| 2c |
| 2c-1 |
| 2c 2 |
| 2c-1 |
∵Tn≤6,∴
| 2c 2 |
| 2c-1 |
∴c2-6c+3≤0,解得3-
| 6 |
| 6 |
∵c∈N,
∴c=2或c=3或c=4或c=5.
点评:本题主要考查了数列的求和问题.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
相关题目
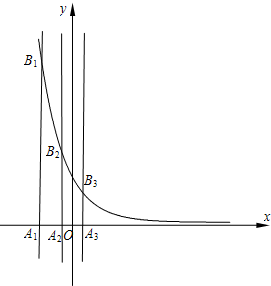 (2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数
(2006•蚌埠二模)已知等差数列{an}的首项为p,公差为d(d>0).对于不同的自然数n,直线x=an与x轴和指数函数