题目内容
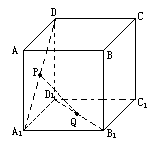
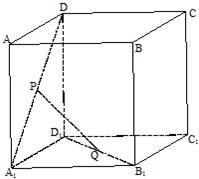
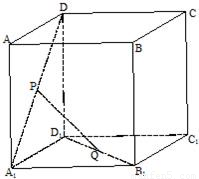
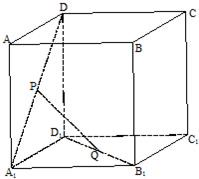 设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.如图:
设P、Q是单位正方体AC1的面AA1D1D、面A1B1C1D1的中心.如图:(1)证明:PQ∥平面AA1B1B;
(2)求线段PQ的长.
分析:(1)取A1B1的中点M,AA1 的中点为N,可证QMNP为平行四边形,故 PQ∥MN,可得PQ∥平面AA1B1B.
(2)在Rt△A1MN 中,由勾股定理可得 MN 的长度,即为PQ 的长度.
(2)在Rt△A1MN 中,由勾股定理可得 MN 的长度,即为PQ 的长度.
解答:(1)证明:取A1B1的中点M,AA1的中点为N,由单位正方体的性质有QM∥A1D1 ,QM=
A1D1.
同理可证PN∥A1D1 ,PN=
A1D1.故QM和PN平行且相等,故QMNP为平行四边形,∴PQ∥MN.
而MN?平面AA1B1B,PQ不在平面AA1B1B 内,故PQ∥平面AA1B1B.
(2)在Rt△A1MN 中,由勾股定理可得MN=
=
=
,
∴PQ=
.
| 1 |
| 2 |
同理可证PN∥A1D1 ,PN=
| 1 |
| 2 |
而MN?平面AA1B1B,PQ不在平面AA1B1B 内,故PQ∥平面AA1B1B.
(2)在Rt△A1MN 中,由勾股定理可得MN=
| A1N2+A1M2 |
|
| ||
| 2 |
∴PQ=
| ||
| 2 |
点评:本题考查证明线面平行的方法,求线段的长度,构造平行四边形QMNP 是解题的关键.

练习册系列答案
相关题目