题目内容
已知 ,
, ,直线
,直线 与函数
与函数 、
、 的图象都相切,且与
的图象都相切,且与 图象的切点为
图象的切点为 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
【答案】
D
【解析】
试题分析:先求出f′(x),求出=f′(1)即其切线l的斜率和切点,代入点斜式求出切线l方程,利用l与g(x)的图象也相切,连立两个方程,则此方程组只有一解,再转化为一个方程一解,等价于判别式△=0,进而求出m的值.解:由题意得,f′(x)= ,g′(x)=x+m,∴与f(x)图象的切点为(1,f(1))的切线l的斜率k=f′(1)=1,且f(1)=ln1=0,所以切点为(1,0),∴直线l的方程为:y=x-1,
,g′(x)=x+m,∴与f(x)图象的切点为(1,f(1))的切线l的斜率k=f′(1)=1,且f(1)=ln1=0,所以切点为(1,0),∴直线l的方程为:y=x-1,
∵直线l与g(x)的图象也相切,∴y=x-1,
此方程组只有一解,即 x2+(m-1)x+
x2+(m-1)x+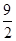 =0只有一解,∴△=(m-1)2-4×
=0只有一解,∴△=(m-1)2-4× ×
×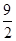 =0,解得m=-2或m=4(舍去).故选D.
=0,解得m=-2或m=4(舍去).故选D.
考点:导数的几何意义
点评:本小题主要考查直线的斜率与导数的几何意义的关系、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力,易错点直线l与两个函数图象相切时切点不同

练习册系列答案
相关题目
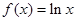 ,
,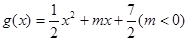 ,直线
,直线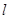 与函数
与函数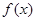 的图象相切,切点的横坐标为
的图象相切,切点的横坐标为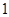 ,且直线
,且直线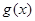 的图象也相切.(Ⅰ)求直线
的图象也相切.(Ⅰ)求直线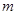 的值;(Ⅱ)若
的值;(Ⅱ)若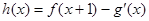 (其中
(其中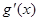 是
是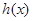 的最大值;(Ⅲ)当
的最大值;(Ⅲ)当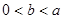 时,求证:
时,求证:
 ,
, ,直线
,直线 与函数
与函数 、
、 的图象都相切,且与函数
的图象都相切,且与函数 .
. 的值;
的值; (其中
(其中 是
是 的最大值;
的最大值; 时,求证:
时,求证: .
.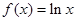 ,
,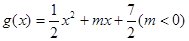 ,直线
,直线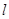 与函数
与函数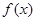 、
、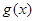 的图象都相切,且与函数
的图象都相切,且与函数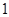 .
.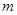 的值;
的值;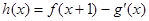 (其中
(其中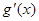 是
是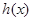 的最大值;
的最大值;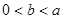 时,求证:
时,求证: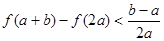 .
.