题目内容
已知二次函数![]() ,满足不等式
,满足不等式![]() 的解集是(-2,0),
的解集是(-2,0),
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)若点![]()
![]() 在函数
在函数![]() 的图象上,且
的图象上,且![]() ,令
,令![]() ,
,
(ⅰ)求证:数列![]() 为等比数列;
为等比数列;
(ⅱ)令![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是
,是![]() 否存在正实数
否存在正实数![]() 使得不等式
使得不等式![]() 对任意
对任意![]() 的恒成立? 若存在,求出
的恒成立? 若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(Ⅰ)![]() 不等式
不等式![]() 的解集是
的解集是![]() ,
,
由韦达定理得![]() ,即
,即![]() ,……………………………………………2分
,……………………………………………2分
![]() ;……………………………………………………………………3分
;……………………………………………………………………3分![]()
(Ⅱ)![]() 点
点![]()
![]() 在函数
在函数![]() 的图象上,
的图象上,![]() ,
,
(ⅰ)![]() ,
,![]() ,
,
即![]()
![]() 数列
数列![]() 为等比数列; ……………………………………………………7分
为等比数列; ……………………………………………………7分
(ⅱ)由(ⅰ)知![]() ,公比为
,公比为![]() ,
,![]()
![]() ;
;
又![]() ,
,
![]() ,
,
![]() ,
,
错位相减得:![]() ,
,
整理得![]() ,……………………………………………………………………9分
,……………………………………………………………………9分
![]() ,即
,即![]() ,
,
化简整理得![]() 对任意
对任意![]() 的恒成立, ………………………………………10分
的恒成立, ………………………………………10分
令![]() ,只要
,只要![]() ,
,
配方得![]() ,
,
![]() ,
,![]() 当
当![]() 时
时![]() ,即
,即![]() .………………………………………12分
.………………………………………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
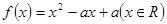 同时满足:①不等式
同时满足:①不等式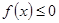 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在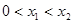 ,使得不等式
,使得不等式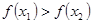 成立.
成立.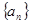 的前
的前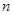 项和
项和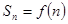 ,
,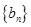 中,令
中,令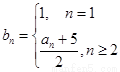 ,
,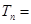
 ,求
,求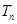 ;
;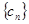 中,所有满足
中,所有满足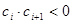 的正整数
的正整数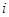 的个数称为这个数列
的个数称为这个数列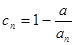 (
(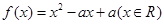 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在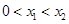 ,使得不等式
,使得不等式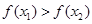 成立,设数列
成立,设数列 的前
的前 项和
项和 。
。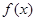 的表达式;
的表达式; 的数列
的数列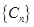 中,所有满足
中,所有满足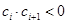 的整数
的整数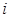 的个数称为这个数列
的个数称为这个数列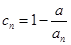 (
(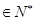 ),求数列
),求数列