题目内容
已知函数
 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是( )
的大小关系是( )

 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时不等式
时不等式 成立, 若
成立, 若 ,
,
 ,则
,则 的大小关系是( )
的大小关系是( )A. | B. |
C. | D.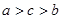 |
C
解:构造函数h(x)=xf(x),
由函数y=f(x)以及函数y=x是R上的奇函数可得h(x)=xf(x)是R上的偶函数,
又当x∈(-∞,0)时h′(x)=f(x)+xf′(x)<0,
所以函数h(x)在x∈(-∞,0)时的单调性为单调递减函数;
所以h(x)在x∈(0,+∞)时的单调性为单调递增函数.
又因为函数y=f(x)是定义在R上的奇函数,所以f(0)=0,从而h(0)=0
因为log31 9 =-2,所以f(log31
9 =-2,所以f(log31  9 )=f(-2)=f(2),
9 )=f(-2)=f(2),
由0<logπ3<1<30.3<30.5<2
所以h(logπ3)<h(30.3)<h(2)=f(log31 9 ),即:b<a<c
9 ),即:b<a<c
故选C.
由函数y=f(x)以及函数y=x是R上的奇函数可得h(x)=xf(x)是R上的偶函数,
又当x∈(-∞,0)时h′(x)=f(x)+xf′(x)<0,
所以函数h(x)在x∈(-∞,0)时的单调性为单调递减函数;
所以h(x)在x∈(0,+∞)时的单调性为单调递增函数.
又因为函数y=f(x)是定义在R上的奇函数,所以f(0)=0,从而h(0)=0
因为log31
 9 =-2,所以f(log31
9 =-2,所以f(log31  9 )=f(-2)=f(2),
9 )=f(-2)=f(2),由0<logπ3<1<30.3<30.5<2
所以h(logπ3)<h(30.3)<h(2)=f(log31
 9 ),即:b<a<c
9 ),即:b<a<c故选C.

练习册系列答案
相关题目

 的定义域; (2)证明函数
的定义域; (2)证明函数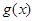 是定义在
是定义在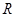 上,且以1为周期的函数,若函数
上,且以1为周期的函数,若函数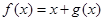 在区间
在区间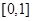 上的值域为
上的值域为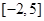 ,则
,则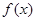 在区间
在区间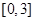 上的值域为________.
上的值域为________. 是函数
是函数 的极大值点,则
的极大值点,则 等于( )
等于( )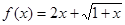 的值域是_______________.
的值域是_______________.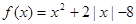 ,定义域为
,定义域为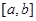
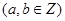 ,值域为
,值域为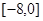 ,则满足条件的整数对
,则满足条件的整数对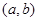 有 对.
有 对.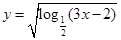 的定义域是( )
的定义域是( )



 的定义域为
的定义域为 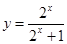 的值域为 .
的值域为 .