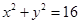题目内容
以原点为圆心,且截直线3x+4y+15=0所得弦长为8的圆的方程是( )A.x2+y2=5
B.x2+y2=16
C.x2+y2=4
D.x2+y2=25
【答案】分析:先求弦心距,再求半径,可得圆的方程.
解答:解:弦心距是: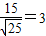 ,弦长为8,所以半径是5
,弦长为8,所以半径是5
所求圆的方程是:x2+y2=25
故选D.
点评:本题考查直线与圆的位置关系,圆的标准方程,是基础题.
解答:解:弦心距是:
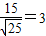 ,弦长为8,所以半径是5
,弦长为8,所以半径是5所求圆的方程是:x2+y2=25
故选D.
点评:本题考查直线与圆的位置关系,圆的标准方程,是基础题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
以原点为圆心,且截直线3x+4y+15=0所得弦长为8的圆的方程是( )
| A、x2+y2=5 | B、x2+y2=16 | C、x2+y2=4 | D、x2+y2=25 |
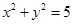 B.
B.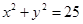
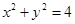 D.
D.