题目内容
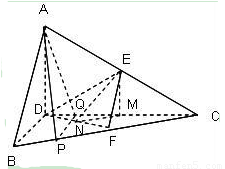
如图,正△ABC的边长为4,CD是AB边上的高,E,F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
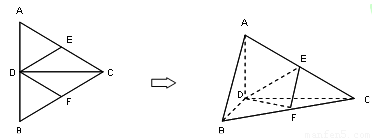
(1)试判断直线AB与平面DEF的位置关系,并说明理由;
(2)求棱锥E-DFC的体积;
(3)在线段BC上是否存在一点P,使AP⊥DE?如果存在,求出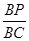 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
【答案】
(1) 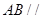 平面
平面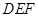 ;(2)
;(2)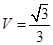 ;(3)
;(3) .
.
【解析】
试题分析:本题主要考查线面垂直、线面平行、线线垂直、线线平行以及锥体体积问题,考查空间想象能力、运算能力和推理论证能力.第一问,在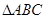 中,利用中位线得到
中,利用中位线得到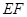 与
与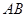 平行,通过线面平行的判断定理即可得到
平行,通过线面平行的判断定理即可得到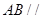 平面
平面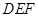 ;第二问,要求三棱锥的体积,找到底面积和高是关键,通过
;第二问,要求三棱锥的体积,找到底面积和高是关键,通过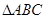 的翻折得出
的翻折得出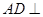 平面
平面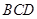 ,通过
,通过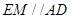 ,得出
,得出 平面
平面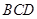 ,所以
,所以 为锥体的高,利用锥体体积公式计算出体积;第三问,在线段
为锥体的高,利用锥体体积公式计算出体积;第三问,在线段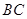 上取点
上取点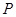 .使
.使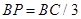 ,
过
,
过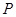 作
作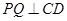 于
于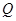 ,在
,在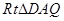 中,利用边长求出
中,利用边长求出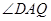 的正切,从而确定角的度数,在等边三角形
的正切,从而确定角的度数,在等边三角形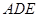 中,
中,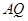 是角平分线,所以
是角平分线,所以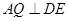 ,再利用线面垂直的判定证出
,再利用线面垂直的判定证出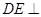 平面
平面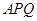 ,所以
,所以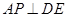 .
.
试题解析:(1)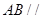 平面
平面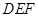 ,理由如下:
,理由如下:
如图:在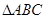 中,由
中,由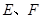 分别是
分别是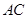 、
、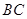 中点,得
中点,得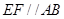 ,
,
又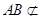 平面
平面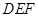 ,
, 平面
平面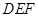 .∴
.∴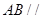 平面
平面 .
.
(2)∵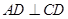 ,
,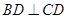 ,将
,将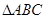 沿
沿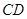 翻折成直二面角
翻折成直二面角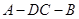 .
.
∴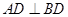 ∴
∴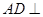 平面
平面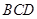
取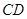 的中点
的中点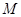 ,这时
,这时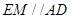 ∴
∴ 平面
平面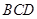 ,
,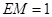 ,
,
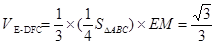
(3)在线段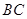 上存在点
上存在点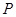 ,使
,使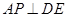
证明如下:在线段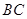 上取点
上取点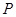 .使
.使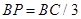 ,
过
,
过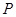 作
作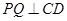 于
于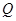 ,
,
∵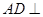 平面
平面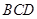 ∴
∴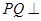 平面
平面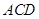
∴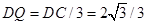 , ∴
, ∴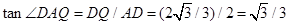 ,
,
∴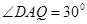 在等边
在等边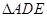 中,
中,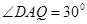 ∴
∴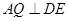
∵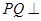 平面
平面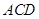 ∴
∴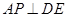 .
.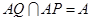
∴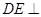 平面
平面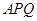 , ∴
, ∴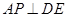 .
.
此时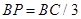 , ∴
, ∴ .
.
考点:1.线面平行的判定定理;2.线面垂直的判定;3.锥体体积公式.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
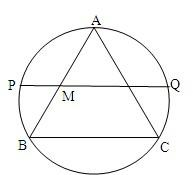 (选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
(选做题)(几何证明选讲)如图,正△ABC的边长为2,点M,N分别是边AB,AC的中点,直线MN与△ABC的外接圆的交点为P、Q,则线段PM=
 如图,正△ABC的边长为15,
如图,正△ABC的边长为15,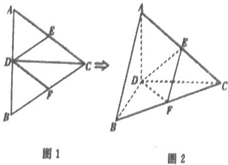 如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.
如图,正△ABC的边长为2a,CD是AB边上的高,E、F分别是AD和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B.