题目内容
直线y=kx+1与圆x2+y2-2y=0的位置关系是
- A.相交
- B.相切
- C.相离
- D.取决于k的值
A
分析：根据圆的方程，先求出圆的圆心和半径，求出圆心到直线y=kx+1的距离，再和半径作比较，可得直线与圆的位置关系．
解答：圆x2+y2-2y=0 即 x2+（y-1）2=1，表示以（0，1）为圆心，半径等于1的圆．
圆心到直线y=kx+1的距离为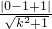
=0，故圆心（0，1）在直线上，故直线和圆相交，
故选A．
点评：本题主要考查求圆的标准方程的特征，直线和圆的位置关系，点到直线的距离公式，属于中档题．
分析：根据圆的方程，先求出圆的圆心和半径，求出圆心到直线y=kx+1的距离，再和半径作比较，可得直线与圆的位置关系．
解答：圆x2+y2-2y=0 即 x2+（y-1）2=1，表示以（0，1）为圆心，半径等于1的圆．
圆心到直线y=kx+1的距离为
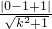=0，故圆心（0，1）在直线上，故直线和圆相交，故选A．
点评：本题主要考查求圆的标准方程的特征，直线和圆的位置关系，点到直线的距离公式，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若直线y=kx+1与圆x2+y2+kx+my-4=0交于M，N两点，且M，N关于直线x-y=0对称，动点P（a，b）在不等式组
表示的平面区域内部及边界上运动，则w=
的取值范围是（ ）
|
| b-2 |
| a-1 |
| A、[2，+∞） |
| B、（-∞，-2] |
| C、[-2，2] |
| D、（-∞，-2]∪[2，+∞） |