题目内容
在一个球的球面上有P、A、B、C、D五个点,且P-ABCD是正四棱锥,同时球心和P点在平面ABCD的异侧,则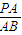 的取值范围是 .
的取值范围是 .
【答案】分析:根据题意,外接球的球心O在高PO1的延长线上,由此可得PO1<AO1,结合Rt△POA1中用勾股定理和正四棱锥的性质,建立关于PA、AB的不等式,解之可得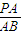 的取值范围.
的取值范围.
解答:解:设底面ABCD的中心为O1,则外接球的球心O在直线PO1上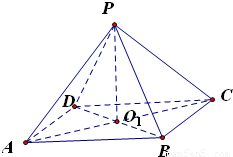
∵球心O和P点在平面ABCD的异侧,
∴球心O在高PO1的延长线上,得PO1<AO1
∵Rt△POA1中,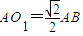 ,
,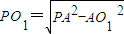 ,
,
∴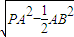
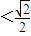 AB,解之得PA<AB,
AB,解之得PA<AB,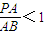
又∵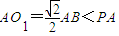 ,∴
,∴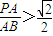 ,
,
由此可得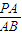 的取值范围:(
的取值范围:(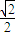 ,1)
,1)
故答案为:(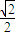 ,1)
,1)
点评:本题给出正四棱锥外接球的球心和顶点在底面的两侧,求侧棱与底面边长比值的取值范围.着重考查了正棱锥的性质和多面体的外接球等知识,属于基础题.
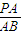 的取值范围.
的取值范围.解答:解:设底面ABCD的中心为O1,则外接球的球心O在直线PO1上

∵球心O和P点在平面ABCD的异侧,
∴球心O在高PO1的延长线上,得PO1<AO1
∵Rt△POA1中,
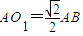 ,
,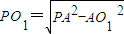 ,
,∴
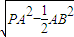
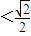 AB,解之得PA<AB,
AB,解之得PA<AB,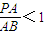
又∵
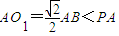 ,∴
,∴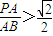 ,
,由此可得
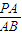 的取值范围:(
的取值范围:(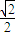 ,1)
,1)故答案为:(
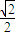 ,1)
,1)点评:本题给出正四棱锥外接球的球心和顶点在底面的两侧,求侧棱与底面边长比值的取值范围.着重考查了正棱锥的性质和多面体的外接球等知识,属于基础题.

练习册系列答案
相关题目