题目内容
如图，“杨辉三角”中从上往下数共有n（n＞7，n∈N）行，设其第k（k≤n，k∈N*）行中不是1的数字之和为ak，由a1，a2，a3，…组成的数列{an}的前n项和是Sn现有下面四个结论：①a8=254；②an=an-1+2n；③S3=22；④Sn=2n+1-2-2n．其中正确结论的序号为（ ）
A．①④
B．②④
C．④
D．①②③④
【答案】分析：①由题意可得，第8行中的数为C8，C81，C82，…C88，则a8=C81+…+C87=28-2，计算可判断①
②由题意可得，an=Cn+Cn1+…+Cnn-2=2n-2，an-1=Cn-1+Cn-11+…+Cn-1n-1=2n-1-2则，代入可检验②
③由题意可得，S3=a1+a2+a3=0+2+6，从而可判断③
④Sn=a1+a2+…+an=（21-2）+（22-2）+…+（2n-1）-1，利用分组求和及等比数列的求和公式可判断④
解答：解：①由题意可得，第8行中的数为C8，C81，C82，…C88，则a8=C81+…+C87=28-2=254，故①正确
②由题意可得，an=Cn+Cn1+…+Cnn-2=2n-2，an-1=Cn-1+Cn-11+…+Cn-1n-1=2n-1-2则an-1+2n=2n-1+2n≠2n，故②错误
③由题意可得，S3=a1+a2+a3=0+2+6=8，故③错误
④Sn=a1+a2+…+an=（21-2）+（22-2）+…+（2n-1）-1=（21+22+…+2n）-2n=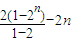
=2n+1-2n-2，故④正确
故选A
点评：本题主要考查 了由杨辉三角求解数列的和，二项式系数的性质的应用，解题的关键是由题目中的定义合理准确的进行求解．
②由题意可得，an=Cn+Cn1+…+Cnn-2=2n-2，an-1=Cn-1+Cn-11+…+Cn-1n-1=2n-1-2则，代入可检验②
③由题意可得，S3=a1+a2+a3=0+2+6，从而可判断③
④Sn=a1+a2+…+an=（21-2）+（22-2）+…+（2n-1）-1，利用分组求和及等比数列的求和公式可判断④
解答：解：①由题意可得，第8行中的数为C8，C81，C82，…C88，则a8=C81+…+C87=28-2=254，故①正确
②由题意可得，an=Cn+Cn1+…+Cnn-2=2n-2，an-1=Cn-1+Cn-11+…+Cn-1n-1=2n-1-2则an-1+2n=2n-1+2n≠2n，故②错误
③由题意可得，S3=a1+a2+a3=0+2+6=8，故③错误
④Sn=a1+a2+…+an=（21-2）+（22-2）+…+（2n-1）-1=（21+22+…+2n）-2n=
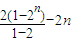=2n+1-2n-2，故④正确故选A
点评：本题主要考查 了由杨辉三角求解数列的和，二项式系数的性质的应用，解题的关键是由题目中的定义合理准确的进行求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
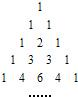如图，在杨辉三角中，从上往下数共有n（n∈N*）行，在这些数中非1的数字之和是
如图，在杨辉三角中（三角形两腰数字为1，其余各项等于两肩数字之和），从上往下共有n行，则这些数中不是1的数字之和为（ ）| A、2n-2n | B、2n-2n+1 | C、2n-1 | D、n2-2n+1 |
杨辉是我国南宋著名的数学家，“杨辉三角”是杨辉的一大重要研究成果，其中蕴含了许多优美的规律（如图），“杨辉三角”中第14行从左到右第10与第11个数的比值为
如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10，…，记其前n项和为Sn，则S21的值为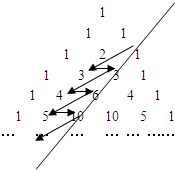
如图，在杨辉三角中，斜线l的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记其n项和为Sn，则S21等于（ ）