题目内容
如图，在杨辉三角中，斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}：1，3，3，4，6，5，10，…，记其前n项和为Sn，则S21的值为361
361
．分析：确定“锯齿形”数列的奇数项、偶数项的通项，直接计算，即可得到结论．
解答：解：由题意，设“锯齿形”数列的奇数项构成数列{bn}，
由b2-b1=3-1=2，b3-b2=6-3=3，b4-b3=10-6=4，b5-b4=15-10=5，可得bn-bn-1=n，
所以可得bn=
+b1，即bn=
，
因为“锯齿形”数列的偶数项构成以3为首项，1为公差的等差数列，
∴S21=1+3+6+10+15+21+28+36+45+55+66+3+4+5+6+7+8+9+10+11+12=361
故答案为：361．
由b2-b1=3-1=2，b3-b2=6-3=3，b4-b3=10-6=4，b5-b4=15-10=5，可得bn-bn-1=n，
所以可得bn=
| (2+n)(n-1) |
| 2 |
| n2+n |
| 2 |
因为“锯齿形”数列的偶数项构成以3为首项，1为公差的等差数列，
∴S21=1+3+6+10+15+21+28+36+45+55+66+3+4+5+6+7+8+9+10+11+12=361
故答案为：361．
点评：本题考查数列的运用，考查数列的求和，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
如图，在杨辉三角中，从上往下数共有n（n∈N*）行，在这些数中非1的数字之和是
如图，在杨辉三角中（三角形两腰数字为1，其余各项等于两肩数字之和），从上往下共有n行，则这些数中不是1的数字之和为（ ）| A、2n-2n | B、2n-2n+1 | C、2n-1 | D、n2-2n+1 |
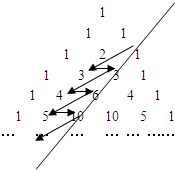如图，在杨辉三角中，斜线l的上方，从1开始箭头所示的数组成一个锯齿形数列：1，3，3，4，6，5，10，…，记其n项和为Sn，则S21等于（ ）
如图，在杨辉三角中，斜线上方的数组成数列：1，3，6，10，…，记这个数列的前n项和为Sn，则