题目内容
已知圆C: .
.
(1)直线 过点P(1,2),且与圆C交于A、B两点,若
过点P(1,2),且与圆C交于A、B两点,若 ,求直线
,求直线 的方程;
的方程;
(2)过圆C上一动点M作平行于y轴的直线m,设直线m与x轴的交点为N,若向量 ,求动点
,求动点 的轨迹方程;
的轨迹方程;
(3) 若点R(1,0),在(2)的条件下,求 的最小值及相应的
的最小值及相应的 点坐标.
点坐标.
(1)3x-4y+5=0或x=1 ;(2)  点的轨迹方程是
点的轨迹方程是 (
( ) ;
) ;
(3)Q的坐标为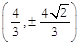 。
。
【解析】(1)分别讨论直线l的斜率存在和不存在两种情况.当斜率不存在时,可根据点到直线的距离公式再结合的圆的弦长公式可求出斜率k值.进而求出直线l的方程.
(2)本小题属于相关点法求动点的轨迹方程,先设出Q点坐标为(x,y), 点M的坐标为( ),然后根据
),然后根据 ,用x,y表示
,用x,y表示 ,再根据点M在圆上,可得到动点Q的轨迹方程.
,再根据点M在圆上,可得到动点Q的轨迹方程.
(3)设Q坐标为(x,y),得 ,再利用点Q的轨迹方程,消去y转化为关于x的一元二次函数来确定其最值,要注意x的取值范围.
,再利用点Q的轨迹方程,消去y转化为关于x的一元二次函数来确定其最值,要注意x的取值范围.
(1)①当直线 垂直于
垂直于 轴时,则此时直线方程为
轴时,则此时直线方程为 ,
, 与圆的两个交点坐标为
与圆的两个交点坐标为
 和
和 ,其距离为
,其距离为 ,满足题意 ………1分
,满足题意 ………1分
②若直线 不垂直于
不垂直于 轴,设其方程为
轴,设其方程为 ,即
,即 ………2分
………2分
设圆心到此直线的距离为 ,则
,则 ,得
,得 ∴
∴ ,
, …4分
…4分
故所求直线方程为3x-4y+5=0
综上所述,所求直线为3x-4y+5=0或x=1 ……………5分
(2)设点M的坐标为( ,
, ),Q点坐标为(x,y)则N点坐标是(
),Q点坐标为(x,y)则N点坐标是( ,0)
,0)
∵ ,∴
,∴ 即
即 ,
,
 ………7分
………7分
又∵ ,∴
,∴ …………9分
…………9分
由已知,直线m //y轴,所以, ,
,
∴ 点的轨迹方程是
点的轨迹方程是 (
( )
……………10分
)
……………10分
(3)设Q坐标为(x,y), ,
,

 ,
…………11分
,
…………11分
又 (
( )可得:
)可得:

 .
………………13分
.
………………13分

此时Q的坐标为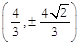 …………14分
…………14分

 . (1)写出圆C的标准方程;(2)是否存在斜率为1的直线m,使m被圆C截得的弦为AB,且以AB为直径的圆过原点.若存在,求出直线m的方程; 若不存在,说明理由.
. (1)写出圆C的标准方程;(2)是否存在斜率为1的直线m,使m被圆C截得的弦为AB,且以AB为直径的圆过原点.若存在,求出直线m的方程; 若不存在,说明理由.