题目内容
（2012•淄博二模）正三角形ABC的边长为2．将它沿高AD翻折，使得平面ABD⊥平面ADC，则三棱锥B-ADC的外接球的表面积为
5π
5π
．分析：三棱锥B-ACD的三条侧棱BD、DC、DA两两互相垂直，它的外接球就是它扩展为长方体的外接球，求出长方体的对角线的长，就是球的直径，然后求球的表面积即可．
解答：解：根据题意可知三棱锥B-ACD的三条侧棱BD、DC、DA两两互相垂直，所以它的外接球就是它扩展为长方体的外接球，
所以求出长方体的对角线的长为：
=
所以球的直径是
，半径为
∴三棱锥B-ADC的外接球的表面积为4π×(
)2=5π
故答案为：5π
所以求出长方体的对角线的长为：
| 1+1+3 |
| 5 |
所以球的直径是
| 5 |
| ||
| 2 |
∴三棱锥B-ADC的外接球的表面积为4π×(
| ||
| 2 |
故答案为：5π
点评：本题考查了外接球的表面积的度量，解题关键将三棱锥B-ACD的外接球扩展为长方体的外接球，属于中档题．
练习册系列答案
相关题目
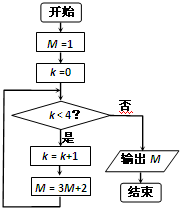（2012•淄博二模）执行如图所示的程序框图，输出的M的值为（ ）