题目内容
(2012•淄博二模)设f(x)是定义在R上的偶函数,对任意的x∈R,都有f(x)=f(x+4),且当x∈[0,2]时,f(x)=2x-1,则方程f(x)-log2(x+2)=0的实数根的个数为
4
4
.分析:由题意可得出函数是周期为4的偶函数且x∈[-2,2]时,f(x)=2|x|-1,由此可作出f(x)在实数集上的图象,又方程f(x)-log2(x+2)=0的实数根的个数即两函数y=f(x)与y=log2(x+2)的图象的交点个数,由此将方程根的个数问题转化为两函数图象交点个数的问题,作图即可得出答案
解答: 解:f(x)是定义在R上的偶函数,当x∈[0,2]时,f(x)=2x-1
解:f(x)是定义在R上的偶函数,当x∈[0,2]时,f(x)=2x-1
∴x∈[-2,2]时,f(x)=2|x|-1
又对任意的x∈R,都有f(x)=f(x+4),故周期是4
方程f(x)-log2(x+2)=0的实数根的个数即两函数y=f(x)与y=log2(x+2)的图象的交点个数
如图,由图知,两函数有四个交点
即方程f(x)-log2(x+2)=0的实数根的个数为4
故答案为4
 解:f(x)是定义在R上的偶函数,当x∈[0,2]时,f(x)=2x-1
解:f(x)是定义在R上的偶函数,当x∈[0,2]时,f(x)=2x-1∴x∈[-2,2]时,f(x)=2|x|-1
又对任意的x∈R,都有f(x)=f(x+4),故周期是4
方程f(x)-log2(x+2)=0的实数根的个数即两函数y=f(x)与y=log2(x+2)的图象的交点个数
如图,由图知,两函数有四个交点
即方程f(x)-log2(x+2)=0的实数根的个数为4
故答案为4
点评:本题考查了根的存在性及根的个数判断,函数的周期性与偶函数的性质,解题的关键是把问题转化为图象问题解决,以形助数是函数类问题的常用方法,学习时要体会总结经验与规律

练习册系列答案
相关题目
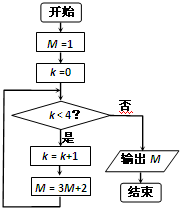 (2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )
(2012•淄博二模)执行如图所示的程序框图,输出的M的值为( )