题目内容
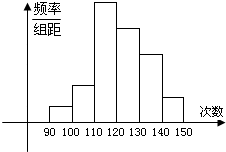为了了解高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12．（1）第二小组的频率是多少？
（2）样本容量是多少？
（3）若次数在110以上为达标，试估计全体高一学生的达标率为多少？
分析：（1）根据从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12，用比值做出样本容量．
（2）第一问做出的样本容量可以把上面的过程写出来．
（3）根据上面做出的样本容量和前两个小长方形所占的比例，用所有的样本容量减去前两个的频数之和，得到结果，除以样本容量得到概率．
（2）第一问做出的样本容量可以把上面的过程写出来．
（3）根据上面做出的样本容量和前两个小长方形所占的比例，用所有的样本容量减去前两个的频数之和，得到结果，除以样本容量得到概率．
解答：解：（1）∵从左到右各小长方形的面积之比为2：4：17：15：9：3，
第二小组频数为12．
∴样本容量是
=150
∴第二小组的频率是
=0.08
（2）样本容量是
=150
（3）∵次数在110以上为达标，
次数在110以上的有150（1-
）=132
∴全体高一学生的达标率为
=0.88
第二小组频数为12．
∴样本容量是
| (2+4+17+15+9+3)×12 |
| 4 |
∴第二小组的频率是
| 12 |
| 150 |
（2）样本容量是
| (2+4+17+15+9+3)×12 |
| 4 |
（3）∵次数在110以上为达标，
次数在110以上的有150（1-
| 6 |
| 50 |
∴全体高一学生的达标率为
| 132 |
| 150 |
点评：本题考查频率分步直方图的应用，是一个基础题，这种题目解题的关键是看清图中所给的条件，知道小长方形的面积就是这组数据的频率．
练习册系列答案
相关题目
，(2)①当k2≤2.706时，可认为两个变量是没有关联的；②当k2＞2.706时，有90％的把握判定两个变量有关联；③当k2＞3.841时，有95％的把握判定两个变量有关联；④当k2＞6.635时，有99％的把握判定两个变量有关联．)为了调查高中学生是否喜欢数学与性别的关系，某班采取分层抽样的方法从2011届高一学生中随机抽出20名学生进行调查，具体情况如下表所示．
| 男 | 女 | |
| 喜欢数学 | 7 | 3 |
| 不喜欢数学 | 3 | 7 |
（参考公式和数据：
（1）
，（2）①当k2≤2.706时，可认为两个变量是没有关联的；②当k2＞2.706时，有90%的把握判定两个变量有关联；③当k2＞3.841时，有95%的把握判定两个变量有关联；④当k2＞6.635时，有99%的把握判定两个变量有关联．）
（Ⅱ）若按下面的方法从这个20个人中抽取1人来了解有关情况：将一个标有数字1，2，3，4，5，6的正六面体骰子连续投掷两次，记朝上的两个数字的乘积为被抽取人的序号，试求：
①抽到号码是6的倍数的概率；
②抽到“无效序号（序号大于20）”的概率．