题目内容
当x>0时,证明不等式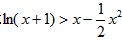 。
。
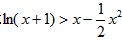 。
。 证明:设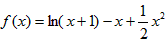 ,
,
则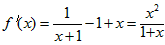 ,
,
当x∈(-1,+∞)时,f′(x)>0,
∴f(x)在(-1,+∞)上是增函数,
于是当x>0时,f(x)>f(0)=0,
∴当x>0时,不等式 成立。
成立。
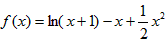 ,
,则
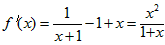 ,
,当x∈(-1,+∞)时,f′(x)>0,
∴f(x)在(-1,+∞)上是增函数,
于是当x>0时,f(x)>f(0)=0,
∴当x>0时,不等式
 成立。
成立。
练习册系列答案
相关题目
题目内容
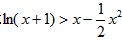 。
。 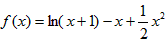 ,
,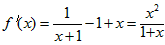 ,
, 成立。
成立。