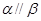题目内容
设m,n是两条不同直线,α,β是两个不同的平面,给出下列四个命题:
①若m?α,n∥α,则m∥n;
②m⊥α,n⊥β,m⊥n,则α⊥β;
③若α∩β=n,m∥n,则m∥α,且m∥β;
④若m⊥α,m⊥β,则α∥β其中正确的命题是( )
①若m?α,n∥α,则m∥n;
②m⊥α,n⊥β,m⊥n,则α⊥β;
③若α∩β=n,m∥n,则m∥α,且m∥β;
④若m⊥α,m⊥β,则α∥β其中正确的命题是( )
分析:本题中四个选项涉及的命题是在线面关系的背景下研究线线、线面位置关系.①②两个选项是在线面平行、面面垂直的背景下研究线线平行与垂直,③④两个选项是在面面相交、平行的背景下研究线线平行与垂直,分别由线面平行、面面垂直的性质进行判断得出正确选项.
解答:解:①选项中的命题是不正确的,因为直线m,n可能不在同一个平面内,故不是正确命题;
②选项中的命题是正确的,因为m⊥α,n⊥β,m⊥n成立时,α,β两平面的关系一定是相互垂直,故是正确选项;
③选项中的命题是不正确的,因为α∩β=n,m∥n时,可能m在α内,或m在β内,故不是正确选项;
④选项中的命题是正确的,因为m⊥α,m⊥β,根据垂直于同一条直线的两个平面一定平行,可得α∥β,是正确选项.
故选D.
②选项中的命题是正确的,因为m⊥α,n⊥β,m⊥n成立时,α,β两平面的关系一定是相互垂直,故是正确选项;
③选项中的命题是不正确的,因为α∩β=n,m∥n时,可能m在α内,或m在β内,故不是正确选项;
④选项中的命题是正确的,因为m⊥α,m⊥β,根据垂直于同一条直线的两个平面一定平行,可得α∥β,是正确选项.
故选D.
点评:本题考查平面之间的位置关系,解题的关键是有着较好的空间想像能力以及对空间中线面,面面位置关系性质熟练掌握,本题是一个易错题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
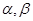 是两个不同的平面,下列命题正确的是( )
是两个不同的平面,下列命题正确的是( )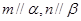 且
且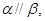 则
则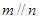 B.
B.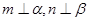 且
且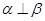 ,则
,则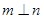
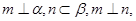 则
则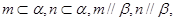 则
则