题目内容
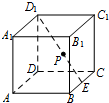 (2013•北京)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为
(2013•北京)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为2
| ||
| 5 |
2
| ||
| 5 |
分析:如图所示,取B1C1的中点F,连接EF,ED1,利用线面平行的性质即可得到C1C∥平面D1EF,进而得到异面直线D1E与C1C的距离.
解答:解:如图所示,取B1C1的中点F,连接EF,ED1,
∵EF
CC1,CC1⊥底面ABCD,∴四边形EFC1C是矩形.
∴CC1∥EF,
又EF?平面D1EF,CC1?平面D1EF,∴CC1∥平面D1EF.
∴直线C1C上任一点到平面D1EF的距离是两条异面直线D1E与CC1的距离.
过点C1作C1M⊥D1F,
∵平面D1EF⊥平面A1B1C1D1.
∴C1M⊥平面D1EF.
过点M作MP∥EF交D1E于点P,则MP∥C1C.
取C1N=MP,连接PN,则四边形MPNC1是矩形.
可得NP⊥平面D1EF,
在Rt△D1C1F中,C1M•D1F=D1C1•C1F,得C1M=
=
.
∴点P到直线CC1的距离的最小值为
.
故答案为

∵EF
| ∥ |
. |
∴CC1∥EF,
又EF?平面D1EF,CC1?平面D1EF,∴CC1∥平面D1EF.
∴直线C1C上任一点到平面D1EF的距离是两条异面直线D1E与CC1的距离.
过点C1作C1M⊥D1F,
∵平面D1EF⊥平面A1B1C1D1.
∴C1M⊥平面D1EF.
过点M作MP∥EF交D1E于点P,则MP∥C1C.
取C1N=MP,连接PN,则四边形MPNC1是矩形.
可得NP⊥平面D1EF,
在Rt△D1C1F中,C1M•D1F=D1C1•C1F,得C1M=
| 2×1 | ||
|
2
| ||
| 5 |
∴点P到直线CC1的距离的最小值为
2
| ||
| 5 |
故答案为
2
| ||
| 5 |
点评:熟练掌握通过线面平行的性质即可得到异面直线的距离是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
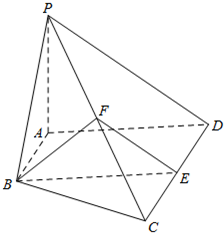 (2013•北京)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点,求证:
(2013•北京)如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD.E和F分别是CD和PC的中点,求证: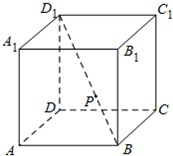 (2013•北京)如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
(2013•北京)如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,P到各顶点的距离的不同取值有( )
 (2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
(2013•北京)如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.