Question

14、某同学对函数f（x）=xcosx进行研究后，得出以下五个结论：①函数y=f（x）的图象是中心对称图形；②对任意实数x，f（x）＞0均成立；③函数[a，b]的图象与x轴有无穷多个公共点，且任意相邻两点的距离相等；④函数y=f（x）的图象与直线y=x有无穷多个公共点，且任意相邻两点的距离相等；⑤当常数k满足|k|＞1时，函数y=f（x）的图象与直线y=kx有且仅有一个公共点．其中所有正确结论的序号是

①④⑤

．

Answer 1

分析：对于①，由于f（-x）=-f（x）是奇函数，函数y=f（x）的图象是中心对称图形，故正确；
先画出原函数f（x）=xcosx的简图．由图可知：②③错；
对于④，根据cosx的周期性，故函数y=f（x）的图象与直线y=x有无穷多个公共点，且任意相邻两点的距离相等．故正确；
对于⑤，因cosx=k．其中|k|＞1时，函数y=f（x）的图象与直线y=kx有且仅有一个公共点（0，0）．从而进行判断即可．

解答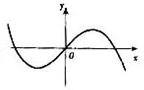：解：先画出原函数f（x）=xcosx的简图．
对于①，由于f（-x）=-xcos（-x）=-xcosx，f（x）=xcosx，
∴f（-x）=-f（x）是奇函数，函数y=f（x）的图象是中心对称图形，故正确；
由图可知：②③错；
对于④，因f（x）=xcosx=x即x=0或cosx=1，其有无穷多个解，根据cosx的周期性，故函数y=f（x）的图象与直线y=x有无穷多个公共点，且任意相邻两点的距离相等．故正确；
对于⑤，因xcosx=kx，即x=0或cosx=k．其中|k|＞1时，函数y=f（x）的图象与直线y=kx有且仅有一个公共点（0，0）．故正确．
故所有正确结论的序号是①④⑤．
故答案为：①④⑤．

点评：本题是基础题，考查三角函数的基本性质，牢记基本知识，基本性质是解好数学题目的关键．