题目内容
在直角坐标平面上,O为原点,M为动点, .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1, .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).(Ⅰ)求曲线C的方程;
(Ⅱ)是否存在直线l,使得|BP|=|BQ|,并说明理由.
【答案】分析:(1)设点T的坐标为(x,y),点M的坐标为(x',y'),进而可知点M1的坐标,进而根据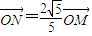 表示出点N的坐标和N1的坐标,进而表示出
表示出点N的坐标和N1的坐标,进而表示出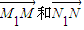 ,进而代入
,进而代入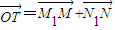 求得x和x'的关系,y和y'的关系,代入
求得x和x'的关系,y和y'的关系,代入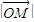 中求得x和y的关系,曲线C的方程可得,判断出曲线C是椭圆.
中求得x和y的关系,曲线C的方程可得,判断出曲线C是椭圆.
(2)当直线l的斜率不存在时,直线l与椭圆C无交点,所以直线l斜率存在,并设为k.直线l的方程为y=k(x-5),直线方程与椭圆方程联立消去y根据判别式大于0求得k的范围,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x,y),进而根据韦达定理表示出x1+x2,进而求得R的坐标,根据|BP|=|BQ|推断BR⊥l,进而可知k•kBR=-1,进而建立等式整理得20k2=20k2-4,结论不可能成立,进而判断不存在直线l,使得|BP|=|BQ|.
解答:解:(Ⅰ)设点T的坐标为(x,y),点M的坐标为(x',y'),则M1的坐标为(0,y'),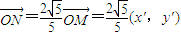 ,于是点N的坐标为
,于是点N的坐标为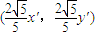 ,N1的坐标
,N1的坐标
为 ,所以
,所以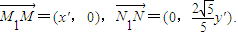
由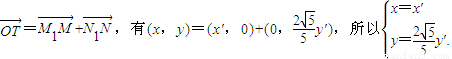
由此得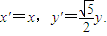
由 ,
,
即所求的方程表示的曲线C是椭圆.
(Ⅱ)点A(5,0)在曲线C即椭圆的外部,当直线l的斜率不存在时,直线l与椭圆C
无交点,所以直线l斜率存在,并设为k.直线l的方程为y=k(x-5).
由方程组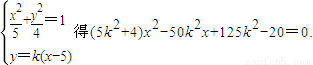
依题意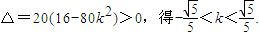
当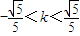 时,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x,y),
时,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x,y),
则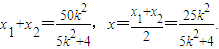 ∴
∴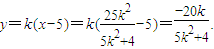
又|BP|=|BQ|?BR⊥l?k•kBR=-1,
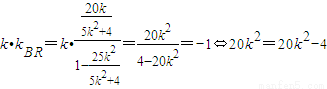 ,
,
而20k2=20k2-4不可能成立,所以不存在直线l,使得|BP|=|BQ|.
点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.当涉及直线与圆锥曲线的位置关系时,常需要把直线方程与圆锥曲线的方程联立,借助韦达定理求得答案.
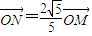 表示出点N的坐标和N1的坐标,进而表示出
表示出点N的坐标和N1的坐标,进而表示出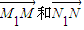 ,进而代入
,进而代入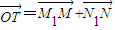 求得x和x'的关系,y和y'的关系,代入
求得x和x'的关系,y和y'的关系,代入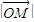 中求得x和y的关系,曲线C的方程可得,判断出曲线C是椭圆.
中求得x和y的关系,曲线C的方程可得,判断出曲线C是椭圆.(2)当直线l的斜率不存在时,直线l与椭圆C无交点,所以直线l斜率存在,并设为k.直线l的方程为y=k(x-5),直线方程与椭圆方程联立消去y根据判别式大于0求得k的范围,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x,y),进而根据韦达定理表示出x1+x2,进而求得R的坐标,根据|BP|=|BQ|推断BR⊥l,进而可知k•kBR=-1,进而建立等式整理得20k2=20k2-4,结论不可能成立,进而判断不存在直线l,使得|BP|=|BQ|.
解答:解:(Ⅰ)设点T的坐标为(x,y),点M的坐标为(x',y'),则M1的坐标为(0,y'),
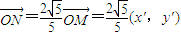 ,于是点N的坐标为
,于是点N的坐标为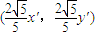 ,N1的坐标
,N1的坐标为
 ,所以
,所以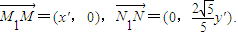
由
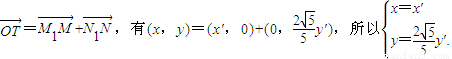
由此得
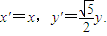
由
 ,
,即所求的方程表示的曲线C是椭圆.
(Ⅱ)点A(5,0)在曲线C即椭圆的外部,当直线l的斜率不存在时,直线l与椭圆C
无交点,所以直线l斜率存在,并设为k.直线l的方程为y=k(x-5).
由方程组
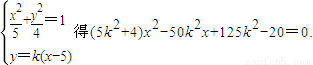
依题意
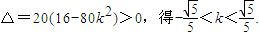
当
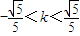 时,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x,y),
时,设交点P(x1,y1),Q(x2,y2),PQ的中点为R(x,y),则
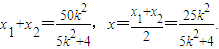 ∴
∴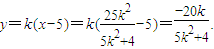
又|BP|=|BQ|?BR⊥l?k•kBR=-1,
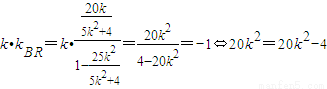 ,
,而20k2=20k2-4不可能成立,所以不存在直线l,使得|BP|=|BQ|.
点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.当涉及直线与圆锥曲线的位置关系时,常需要把直线方程与圆锥曲线的方程联立,借助韦达定理求得答案.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

 .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1, .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).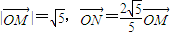 .过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,
.过点M作MM1⊥y轴于M1,过N作NN1⊥x轴于点N1,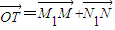 .记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).
.记点T的轨迹为曲线C,点A(5,0)、B(1,0),过点A作直线l交曲线C于两个不同的点P、Q(点Q在A与P之间).