题目内容
若f(x)=tan ,则 ( )
,则 ( )
| A.f(0)>f(-1)>f(1) | B.f(0)>f(1)>f(-1) |
| C.f(1)>f(0)>f(-1) | D.f(-1)>f(0)>f(1) |
C.
解析试题分析:由 得
得 ,
,
所以f(x)在区间 上单调递增,因为
上单调递增,因为 .
.
考点:正切函数的单调性.
点评:本小题关键是利用正切函数的单调区间求出f(x)的单调区间,然后根据单调性比较f(0),f(1),f(-1)的大小。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将函数 的图像左移
的图像左移 ,再将图像上各点横坐标压缩到原来的
,再将图像上各点横坐标压缩到原来的 ,则所得到的图象的解析式为( )
,则所得到的图象的解析式为( )
A. | B. |
C. | D. |
若角 的终边在直线
的终边在直线 上,则
上,则 等于( )
等于( )
A. | B. | C. | D. |
设函数 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )
A.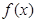 在 在 单调递减 单调递减 | B.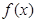 在 在 单调递减 单调递减 |
C.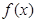 在 在 单调递增 单调递增 | D.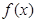 在 在 单调递增 单调递增 |
要得到 的图象,只需将
的图象,只需将 的图象( ).
的图象( ).
A.向左平移 个单位 个单位 | B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 | D.向右平移 个单位 个单位 |
把-495°表示成k×360°+θ(k∈Z)的形式,则θ可以是( )
| A.-135° | B.45° | C.-225° | D.135° |
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |

 是实数,则函数
是实数,则函数 的图象不可能是( )
的图象不可能是( )