题目内容
设函数 的最小正周期为
的最小正周期为 ,且
,且 ,则( )
,则( )
A.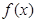 在 在 单调递减 单调递减 | B.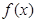 在 在 单调递减 单调递减 |
C.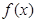 在 在 单调递增 单调递增 | D.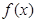 在 在 单调递增 单调递增 |
A
解析试题分析:因为函数f(x)=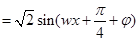 ,根据最小正周期为
,根据最小正周期为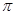 ,则可知w=2,那么得到解析式为f(x)=
,则可知w=2,那么得到解析式为f(x)= ,又因为f(-x) =f(x),说明函数是偶函数,则可知
,又因为f(-x) =f(x),说明函数是偶函数,则可知 ,得到
,得到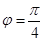 ,故有
,故有 ,故当
,故当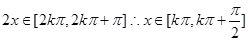 是递减函数,故结合正弦函数的单调区间得到结论选A.
是递减函数,故结合正弦函数的单调区间得到结论选A.
考点:本题主要是考查三角函数的图像与性质的运用。
点评:解决该试题的关键是理解函数的周期性得到w的值,同时将原函数化为单一三角函数,并结合偶函数的定义,得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 =
= ,
, ,则
,则 为( )
为( )
A. | B. | C. | D. |
已知扇形的周长为12  ,面积为8
,面积为8  ,则扇形圆心角的弧度数为( )
,则扇形圆心角的弧度数为( )
| A.1 | B.4 | C.1或4 | D.2或4 |
若 的值是( )
的值是( )
A. | B.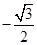 | C. | D. |
 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
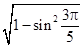 化简的结果是( ).
化简的结果是( ).
A.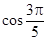 | B.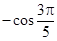 | C.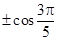 | D.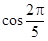 |
若f(x)=tan ,则 ( )
,则 ( )
| A.f(0)>f(-1)>f(1) | B.f(0)>f(1)>f(-1) |
| C.f(1)>f(0)>f(-1) | D.f(-1)>f(0)>f(1) |
设角 的终边经过点
的终边经过点 ,那么
,那么
A. | B. | C. | D. |
函数 在其定义域上是( )
在其定义域上是( )
| A.奇函数 | B.偶函数 | C.增函数 | D.减函数 |