题目内容
定义F(x,y)=(1+x)y,x,y∈(0,+∞).
(1)令函数f(x)=F(1,log2(x3+ax2+bx+1))的图象为曲线C,若存在实数b使得曲线C在x0(-4<x0<-1)处有斜率为-8的切线,求实数a的取值范围;
(2)令函数g(x)=F(1,log2[(lnx-1)ex+x]),是否存在实数x0∈[1,e],使曲线y=g(x)在点x=x0处的切线与y轴垂直?若存在,求出x0的值;若不存在,请说明理由;
(3)当x,y∈N*,且x<y时,求证:F(x,y)>F(y,x).
解析:
|
(1)f(x)=F(1,log2(x3+ax2+bx+1))=x3+ax2+bx+1,设曲线C在x0(-4<x0<-1)处有斜率为-8的切线, 又由题设知log2(x3+ax2+bx+1)>0,令 ∴存在实数b使得 由①得b=-8-3x02-2ax0,代入③得-2x02-ax0-8<0, ∴由 得2×(-4)2+a×(-4)+8>0或2×(-1)2+a×(-1)+8>0, ∴a<10或a<10,∴a<10. 5分 (2)∵g(x)=(lnx-1)ex+x, ∴ 设 当x∈[1,e]时,h′(x)≥0,h(x)为增函数, 因此h(x)在区间[1,e]上的最小值为ln1=0,即 当x0∈[1,e]时, ∴ 曲线y=g(x)在点x=x0处的切线与y轴垂直等价于方程 而 故不存在实数x0∈[1,e],使曲线y=g(x)在点x=x0处的切线与y轴垂直. 9分 (3)令 又令 ∴p(x)在[0,+∞)上单调递减,∴当x>0时,有p(x)<p(0)=0, ∴当x≥1时,有 ∴当1≤x<y时,有 ∴yln(1+x)>xln(1+y),∴(1+x)y>(1+y)x, ∴当x,y∈N*,且x<y时,F(x,y)>F(y,x). 13分 |

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案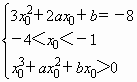 有解. 3分
有解. 3分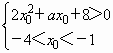 有解,
有解,