题目内容
已知数列的通项公式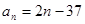 ,则
,则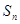 取最小值时
取最小值时 = ,
= ,
此时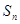 = .
= .
18 -324
解析试题分析:由an=2n﹣37,知{an}是首项为﹣35,公差为2的等差数列,故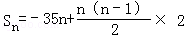 =n2﹣36n=(n﹣18)2﹣324,由此能得到当n=18时,Sn取最小值﹣324.解:∵an=2n﹣37,∴a1=2﹣37=﹣35,a2=4﹣37=﹣33,d=a2﹣a1=33+35=2,∴{an}是首项为﹣35,公差为2的等差数列,∴
=n2﹣36n=(n﹣18)2﹣324,由此能得到当n=18时,Sn取最小值﹣324.解:∵an=2n﹣37,∴a1=2﹣37=﹣35,a2=4﹣37=﹣33,d=a2﹣a1=33+35=2,∴{an}是首项为﹣35,公差为2的等差数列,∴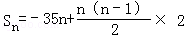 =n2﹣36n=(n﹣18)2﹣324,∴当n=18时,Sn取最小值S18=﹣324.故答案为:18,﹣324.
=n2﹣36n=(n﹣18)2﹣324,∴当n=18时,Sn取最小值S18=﹣324.故答案为:18,﹣324.
考点:等差数列的前n项和
点评:本题考查等差数列的前n项和的性质和应用,是基础题.解题时要认真审题,仔细解答,注意配方法的合理运用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 的前
的前 项和为
项和为 ,若
,若 ,且
,且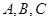 三点共线(该直线不过点
三点共线(该直线不过点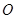 ),则
),则 _____________.
_____________.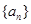 满足
满足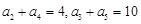 ,则它的前10项和
,则它的前10项和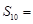 ______
______  满足
满足 ,则
,则 的值等于 。
的值等于 。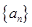 中,若
中,若 ,则该数列的前2009项的和是 .
,则该数列的前2009项的和是 .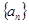 中,
中,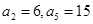 ,若
,若 ,则数列
,则数列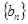 的前5项和等于 .
的前5项和等于 . 和
和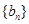 都是等差数列,且
都是等差数列,且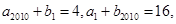 则数列
则数列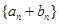 的前2010项的和是 .
的前2010项的和是 .