题目内容
 已知程序框图如图所示,将输出的a的值依次记为a1,a2,…,an,其中n∈N*.且n≤2012,
已知程序框图如图所示,将输出的a的值依次记为a1,a2,…,an,其中n∈N*.且n≤2012,请回答下列问题:
(Ⅰ)将空格
①
①
处填上适当的整数,该整数是多少?(Ⅱ)写出an与n的关系式;
(III)设bn=
| n | 2 |
分析:(Ⅰ)因为框图将输出的a的值依次记为a1,a2,…,an,其中n∈N*.且n≤2012,再根据判断框中的条件满足时结束循环,所以判断框内的条件应是n>2012;
(Ⅱ)由执行框中的运算表达式知,输出的数列是以2为首项,以3为公比的等比数列;
(Ⅲ)把数列{an}的通项代入表达式后,运用错位相减法求数列{bn}的前n项和.
(Ⅱ)由执行框中的运算表达式知,输出的数列是以2为首项,以3为公比的等比数列;
(Ⅲ)把数列{an}的通项代入表达式后,运用错位相减法求数列{bn}的前n项和.
解答:解:(Ⅰ)因为n赋值为1时输出的a=2即a1,该数列共有2012项,所以n>2012时算法结束,共输出2012项;
(Ⅱ)由执行框中的算式看出,该数列是以2为首项,以3为公比的等比数列,所以an=2•3n-1(n≤2012);
(Ⅲ)由bn=
an=
•2•3n-1=n•3n-1
所以Sn=b1+b2+b3+…+bn=1×30+2×31+3×32+…+n×3n-1①
所以3Sn=3+2×32+3×33+…+(n-1)×3n-1+n×3n②
①-②得 -2Sn=(30+31+32+…+3n-1)-n×3n
整理得:Sn=
+
n∈N*.且n≤2012.
(Ⅱ)由执行框中的算式看出,该数列是以2为首项,以3为公比的等比数列,所以an=2•3n-1(n≤2012);
(Ⅲ)由bn=
| n |
| 2 |
| n |
| 2 |
所以Sn=b1+b2+b3+…+bn=1×30+2×31+3×32+…+n×3n-1①
所以3Sn=3+2×32+3×33+…+(n-1)×3n-1+n×3n②
①-②得 -2Sn=(30+31+32+…+3n-1)-n×3n
整理得:Sn=
| 1-3n |
| 4 |
| n•3n |
| 2 |
点评:本题考查了循环结构,训练了错位相减的求和方法,求一个等差数列和一个等比数列的积数列的前n项和,往往是用错位相减法.

练习册系列答案
相关题目
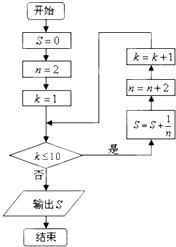
已知程序框图如图所示,则该程序框图的功能是( )

A、求数列{
| ||
B、求数列{
| ||
C、求数列{
| ||
D、求数列{
|
 (2013•内江二模)已知程序框图如图所示,则执行该程序后输出的结果是( )
(2013•内江二模)已知程序框图如图所示,则执行该程序后输出的结果是( ) (2013•内江一模)已知程序框图如图所示,则执行该程序后输出的结果是
(2013•内江一模)已知程序框图如图所示,则执行该程序后输出的结果是 (2012•石家庄一模)已知程序框图如图所示,当输入2与-2时,输出的值均为10,则输入1时输出的值为( )
(2012•石家庄一模)已知程序框图如图所示,当输入2与-2时,输出的值均为10,则输入1时输出的值为( )