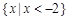题目内容
(本小题满分16分)
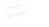 已知函数f(x)=x2-2ax+a+2,aÎR.
已知函数f(x)=x2-2ax+a+2,aÎR.
(1)若不等式f(x)<0的解集为Æ,求实数a的取值范围;
(2)若不等式f(x)≥a对于xÎ[0,+∞)恒成立,求实数a的取值范围.
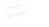 已知函数f(x)=x2-2ax+a+2,aÎR.
已知函数f(x)=x2-2ax+a+2,aÎR.(1)若不等式f(x)<0的解集为Æ,求实数a的取值范围;
(2)若不等式f(x)≥a对于xÎ[0,+∞)恒成立,求实数a的取值范围.
(1)[-1,2].(2)a≤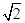 .
.
 .
.本试题主要是考查了一元二次不等式的解集的求解,以及二次不等式的恒成立问题的综合运用。
(1)首先根据二次不等式的解集为空集,说明了判别式小于等于零,从而得到参数的取值范围。
(2)根据不等式f(x)≥a可化为x2-2ax+2≥0对于xÎ[0,+∞)恒成立,然后分析函数g(x)= x2-2ax+2,在给定区间的最小值即可。
解: (1)若不等式f(x)<0的解集为Æ,
则方程f(x)=0的判别式∆≤0, ··········· 2分
即∆=(-2a)2-4(a+2)≤0⇒a2-a-2≤0⇒-1≤a≤2,
所以实数a的取值范围是[-1,2]. ··········· 7分
(2)不等式f(x)≥a可化为x2-2ax+2≥0对于xÎ[0,+∞)恒成立,
令g(x)= x2-2ax+2,函数g(x)的对称轴为x=a,(借助函数图象)········· 9分
当a≥0时,则只需g(a)= a2-2a2+2= -a2+2≥0
⇒-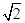 ≤a≤
≤a≤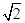 ,即0≤a≤
,即0≤a≤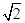 ; ··················· 12分
; ··················· 12分
当a<0时,则只需g(0)=2>0恒成立,此时a<0; ··········· 14分
综上,实数a的取值范围为a≤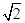 . ·········· 16分
. ·········· 16分
(注:第(2)小题也可以用分离参数的方法来求解)
(1)首先根据二次不等式的解集为空集,说明了判别式小于等于零,从而得到参数的取值范围。
(2)根据不等式f(x)≥a可化为x2-2ax+2≥0对于xÎ[0,+∞)恒成立,然后分析函数g(x)= x2-2ax+2,在给定区间的最小值即可。
解: (1)若不等式f(x)<0的解集为Æ,
则方程f(x)=0的判别式∆≤0, ··········· 2分
即∆=(-2a)2-4(a+2)≤0⇒a2-a-2≤0⇒-1≤a≤2,
所以实数a的取值范围是[-1,2]. ··········· 7分
(2)不等式f(x)≥a可化为x2-2ax+2≥0对于xÎ[0,+∞)恒成立,
令g(x)= x2-2ax+2,函数g(x)的对称轴为x=a,(借助函数图象)········· 9分
当a≥0时,则只需g(a)= a2-2a2+2= -a2+2≥0
⇒-
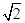 ≤a≤
≤a≤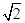 ,即0≤a≤
,即0≤a≤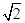 ; ··················· 12分
; ··················· 12分当a<0时,则只需g(0)=2>0恒成立,此时a<0; ··········· 14分
综上,实数a的取值范围为a≤
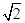 . ·········· 16分
. ·········· 16分(注:第(2)小题也可以用分离参数的方法来求解)

练习册系列答案
相关题目
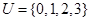 ,
,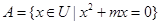 ,若C
,若C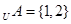 ,则实数
,则实数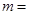 ________.
________.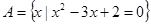 ,
,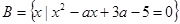 .若A∩B=B,求实数
.若A∩B=B,求实数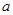 的取值范围.
的取值范围.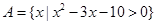 ,
,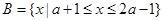 ,
,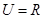 ,且
,且 ,求实数
,求实数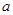 的取值范围
的取值范围 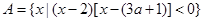 ,
,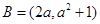
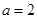 时,求
时,求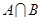 ;
; 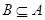 的实数
的实数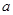 的取值范围(12分)
的取值范围(12分)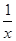 ,x∈R且x≠0},则(ðRB)∩A=
,x∈R且x≠0},则(ðRB)∩A=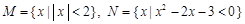 ,则集合
,则集合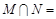 ( )
( )