题目内容
下列说法中正确的序号是________.
①如果命题“?p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②“若a2+b2=0,则a=0且b=0”的否命题是“若a2+b2≠0,则a≠0且b≠0”;
③若?p是q的必要条件,则p是?q的充分条件;
④命题p:x2-8x-20>0和命题q:x2-x-6≥0,则?p是?q的必要不充分条件.
①③④
分析:①由p与¬p必一真一假.由命题“p∨q”是真命题,只要p或q是真命题即可.据此可判断出答案.
②“a=0且b=0”的否定应为“a≠0或b≠0”.
③由¬p是q的必要条件,得q?¬p,其逆否命题为:p?¬q,据此可判断其真假.
④先由已知写出¬p、¬q,再进行判断即可.
解答:①∵命题“?p”是真命题,∴命题p是假命题;又命题“p∨q”是真命题,p与q中至少有一个是真命题,
而命题p是假命题,∴命题q必是真命题.故①正确.
②“若a2+b2=0,则a=0且b=0”的否命题应是“若a2+b2≠0,则a≠0或b≠0”,故②不正确.
③∵?p是q的必要条件,∴q?¬p;其逆否命题为:p?¬q,∴p是?q的充分条件.故③正确.
④由P得:∵x2-8x-20>0,∴其解集为{x|x>10,或x<-2},∴¬p:{x|-2≤x≤10}.
由q得:∵x2-x-6≥0,∴其解集为{x|x≥3,或x≤-2},∴¬q:{x|-2<x<3}.
∴¬q?¬p,而由¬p推不出¬q.∴?p是?q的必要不充分条件.故④正确.
故答案为①③④.
点评:本题综合考查了四种命题间的关系、充要条件和复合命题,深刻理解以上知识是解决问题的关键.
分析:①由p与¬p必一真一假.由命题“p∨q”是真命题,只要p或q是真命题即可.据此可判断出答案.
②“a=0且b=0”的否定应为“a≠0或b≠0”.
③由¬p是q的必要条件,得q?¬p,其逆否命题为:p?¬q,据此可判断其真假.
④先由已知写出¬p、¬q,再进行判断即可.
解答:①∵命题“?p”是真命题,∴命题p是假命题;又命题“p∨q”是真命题,p与q中至少有一个是真命题,
而命题p是假命题,∴命题q必是真命题.故①正确.
②“若a2+b2=0,则a=0且b=0”的否命题应是“若a2+b2≠0,则a≠0或b≠0”,故②不正确.
③∵?p是q的必要条件,∴q?¬p;其逆否命题为:p?¬q,∴p是?q的充分条件.故③正确.
④由P得:∵x2-8x-20>0,∴其解集为{x|x>10,或x<-2},∴¬p:{x|-2≤x≤10}.
由q得:∵x2-x-6≥0,∴其解集为{x|x≥3,或x≤-2},∴¬q:{x|-2<x<3}.
∴¬q?¬p,而由¬p推不出¬q.∴?p是?q的必要不充分条件.故④正确.
故答案为①③④.
点评:本题综合考查了四种命题间的关系、充要条件和复合命题,深刻理解以上知识是解决问题的关键.

练习册系列答案
相关题目
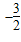 的定义域是{x|x≠0};
的定义域是{x|x≠0};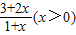 的值域是(2,3);
的值域是(2,3);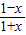 在定义域上为奇函数;
在定义域上为奇函数;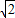 ,则3x-3-x的值为2.
,则3x-3-x的值为2. .
.