题目内容
袋中有大小相同的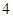 个红球和
个红球和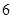 个白球,随机从袋中取
个白球,随机从袋中取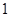 个球,取后不放回,那么恰好在第
个球,取后不放回,那么恰好在第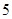 次取完红球的概率是
次取完红球的概率是
A.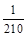 | B.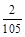 | C.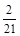 | D.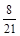 |
B
解析试题分析:恰好在第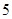 次取完红球说明在前4次取球的过程中有三次取到红球,一次取到白球,当第一次取到白球,第二、三、四、五此都取到白球的概率为
次取完红球说明在前4次取球的过程中有三次取到红球,一次取到白球,当第一次取到白球,第二、三、四、五此都取到白球的概率为 ,当第二次取到红球,第一、三、四、五此都取到白球的概率为
,当第二次取到红球,第一、三、四、五此都取到白球的概率为 ,同理可求第三次、第四次取到红球的概率,几种情况下的概率相加可得恰好在第5次取完红球的概率为
,同理可求第三次、第四次取到红球的概率,几种情况下的概率相加可得恰好在第5次取完红球的概率为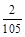 .
.
考点:本题考查排列组合、古典概型等基础知识,考查分析问题解决问题的能力,较难题.
点评:解决概率问题关键是搞清楚属于哪种概率模型,一般要分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设随机变量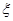 服从正态分 布
服从正态分 布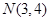 ,若
,若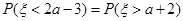 ,则
,则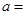 ( )
( )
A.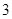 | B. | C.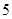 | D.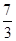 |
同时掷两枚骰子,所得点数之和为5的概率为 ( )
A. | B. | C. | D. |
设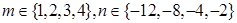 ,则函数
,则函数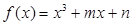 在区间
在区间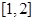 上有零点的概率是( )
上有零点的概率是( )
A.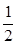 | B.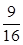 | C.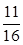 | D. |
从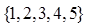 中随机选取一个数为
中随机选取一个数为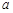 ,从
,从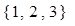 中随机选取一个数为
中随机选取一个数为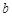 ,则
,则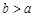 的概率是 ( )
的概率是 ( )
A.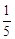 | B.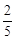 | C.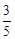 | D.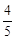 |
 B.
B.  C.
C. 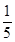 D.
D. 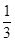
 .质点P移动5次后位于点(2,3)的概率是( )
.质点P移动5次后位于点(2,3)的概率是( )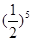
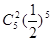
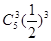
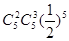
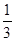 ,乙解决这个问题的概率是
,乙解决这个问题的概率是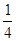 ,那么其中至少有一人解决这个问题的概率是
,那么其中至少有一人解决这个问题的概率是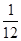
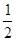
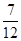
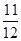
 表示这5人中“三好学生”的人数,则下列概率中等于
表示这5人中“三好学生”的人数,则下列概率中等于 的是( )
的是( )


