题目内容
已知点O、N、P在△ABC所在平面内，且|
|=|
|=|
|，
+
+
=
，
•
=
•
=
•
，则点O、N、P依次为△ABC的（ ）
| OA |
| OB |
| OC |
| NA |
| NB |
| NC |
| 0 |
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
| A、重心、外心、垂心 |
| B、重心、外心、内心 |
| C、外心、重心、垂心 |
| D、外心、重心、内心 |
分析：根据O到三角形三个顶点的距离相等，得到O是三角形的外心，根据所给的四个选项，第一个判断为外心的只有C，D两个选项，只要判断第三个条件可以得到三角形的什么心就可以，移项相减，得到垂直，即得到P是三角形的垂心．
解答：证明：∵|
|=|
|=|
|，
∴O到三角形三个顶点的距离相等，
∴O是三角形的外心，
根据所给的四个选项，第一个判断为外心的只有C，D两个选项，
∴只要判断第三个条件可以得到三角形的什么心就可以，
∵
•
=
•
=
•
，
∴
(
-
)=0，
∴
•
=0，
∴
⊥
，
同理得到另外两个向量都与相对应的边垂直，
得到P是三角形的垂心，
故选C．
| OA |
| OB |
| OC |
∴O到三角形三个顶点的距离相等，
∴O是三角形的外心，
根据所给的四个选项，第一个判断为外心的只有C，D两个选项，
∴只要判断第三个条件可以得到三角形的什么心就可以，
∵
| PA |
| PB |
| PB |
| PC |
| PC |
| PA |
∴
| PB |
| PA |
| PC |
∴
| PB |
| CA |
∴
| PB |
| CA |
同理得到另外两个向量都与相对应的边垂直，
得到P是三角形的垂心，
故选C．
点评：本题是一个考查的向量的知识点比较全面的题目，把几种三角形的心总结的比较全面，解题时注意向量的有关定律的应用，不要在运算律上出错．
练习册系列答案
相关题目
所在平面内，且
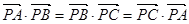，则点O、N、P依次是
，
，
=
=
，则点O、N、P依次为△ABC的（ ）