题目内容
一个扇形OAB的面积是1平方厘米，它的周长是4厘米，求∠AOB和弦AB的长.
∠AOB＝2 rad.该AB的长为2sin1厘米
欲求∠AOB，需要知道
的长和半径OA的长，用弧度制下的弧长公式和扇形面积公式，结合已知条件，能比较容易地求得，之后在△AOB中求弦AB的长.作OM⊥AB交AB于M，则AM＝BM＝AB，在Rt△AMO中求AM.
解：设扇形的半径为R cm.∠AOB=α rad.
据题意
解之得
过O作OM⊥AB交AB于M.
则AM＝BM＝AB.
在Rt△AMO中，AM＝sin1，∴AB＝2sin1
故∠AOB＝2 rad.该AB的长为2sin1厘米.
的长和半径OA的长，用弧度制下的弧长公式和扇形面积公式，结合已知条件，能比较容易地求得，之后在△AOB中求弦AB的长.作OM⊥AB交AB于M，则AM＝BM＝AB，在Rt△AMO中求AM.解：设扇形的半径为R cm.∠AOB=α rad.
据题意
解之得过O作OM⊥AB交AB于M.
则AM＝BM＝AB.
在Rt△AMO中，AM＝sin1，∴AB＝2sin1
故∠AOB＝2 rad.该AB的长为2sin1厘米.
练习册系列答案
相关题目
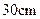，当它的半径和圆心角各取什么值时，才能使扇形的面积最大？最大面积是多少？
－α)＝
，则cos(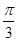
＋α)等于( )
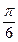
的终边过点
，且
，则
的值为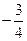
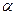是第三象限的角，
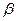是第二象限的角，则
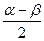是第 象限的角.
，则
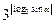等于（ ）
