题目内容
2.已知向量$\overrightarrow{m}$=(sin2x,-1),向量$\overrightarrow{n}$=($\sqrt{3}$cos2x,-$\frac{1}{2}$),函数f(x)=($\overrightarrow{m}$+$\overrightarrow{n}$)•$\overrightarrow{m}$.(Ⅰ)求f(x)的最小正周期T;
(Ⅱ)已知a、b、c分别为△ABC内角A、B、C的对边,A为锐角,a=$\sqrt{13}$,c=2,且f(A)恰是f(x)在[0,$\frac{π}{4}$]上的最大值,求A和b.
分析 (Ⅰ)先求出向量$\overrightarrow{m}+\overrightarrow{n}$的坐标,进行数量积的运算,并根据二倍角的正余弦公式及两角差的正弦公式便可得出f(x)=$sin(4x-\frac{π}{6})+2$,从而可以得出最小正周期T;
(Ⅱ)根据x的范围可求出$4x-\frac{π}{6}$的范围,从而根据正弦函数的图象便可得出x=$\frac{π}{6}$时,f(x)在[0,$\frac{π}{4}$]上取得最大值,从而得出A=$\frac{π}{6}$,然后在△ABC中由余弦定理即可得出b的值.
解答 解:(Ⅰ)$\overrightarrow{m}+\overrightarrow{n}=(sin2x+\sqrt{3}cos2x,-\frac{3}{2})$,$(\overrightarrow{m}+\overrightarrow{n})•\overrightarrow{m}=si{n}^{2}2x+\sqrt{3}sin2xcos2x+\frac{3}{2}$=$\frac{1-cos4x}{2}+\frac{\sqrt{3}}{2}sin4x+\frac{3}{2}$=$sin(4x-\frac{π}{6})+2$;
∴$f(x)=sin(4x-\frac{π}{6})+2$;
∴$T=\frac{2π}{4}=\frac{π}{2}$;
(Ⅱ)$f(x)=sin(4x-\frac{π}{6})+2$,x$∈[0,\frac{π}{4}]$时,$-\frac{π}{6}≤4x-\frac{π}{6}≤\frac{5π}{6}$;
∴$4x-\frac{π}{6}=\frac{π}{2}$时,f(x)取最大值3,此时$x=\frac{π}{6}$;
∴由A是锐角,f(A)=3得,A=$\frac{π}{6}$;
∴由余弦定理得:a2=b2+c2-2bccosA;
∴$13={b}^{2}+4-2\sqrt{3}b$;
解得$b=3\sqrt{3}$,或-$\sqrt{3}$(舍去);
∴$A=\frac{π}{6},b=3\sqrt{3}$.
点评 考查向量加法、数量积的坐标运算,二倍角的正余弦公式,两角差的正弦公式,以及函数y=Asin(ωx+φ)的周期公式,正弦函数在闭区间上的最大值,余弦定理,要熟悉正弦函数图象.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| A. | ${a_n}=\frac{n}{n+1}({n∈{N^*}})$ | B. | ${a_n}={n^2}-1({n∈{N^*}})$ | ||
| C. | ${a_n}=5n+{({-1})^n}({n∈{N^*}})$ | D. | ${a_n}=3n-1({n∈{N^*}})$ |
| A. | ?x∈R,都有x2=1 | B. | ?x0∉R,使得x2=1 | C. | ?x∈R,都有x2≠1 | D. | ?x0∈R,使得x2≠1 |
| A. | A0与A2 | B. | A1与A2 | C. | A1与A3 | D. | A0与A3 |
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
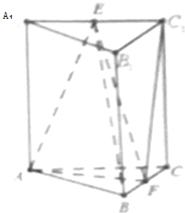 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,E,F分别为A1C1,BC的中点,AA1=3,AC=2,BC=1,AB⊥BC.