题目内容
 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
解析试题分析:设命题p: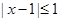 ,命题q:
,命题q: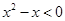 ;由于
;由于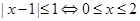 ,
, ,所以
,所以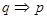 ,但
,但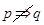 ,故p是q的必要不充分条件.
,故p是q的必要不充分条件.
考点:必要条件、充分条件与充要条件的判断.

练习册系列答案
相关题目
已知命题p:?x∈[0, ],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
],cos2x+cosx-m=0的否定为假命题,则实数m的取值范围是( )
A.[- ,-1] ,-1] |
B.[- ,2] ,2] |
| C.[-1,2] |
D.[- ,+∞) ,+∞) |
下面几个命题中,假命题是( )
A.“若 ,则 ,则 ”的否命题; ”的否命题; |
B.“ ,函数 ,函数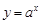 在定义域内单调递增”的否定; 在定义域内单调递增”的否定; |
C.“ 是函数 是函数 的一个周期”或“ 的一个周期”或“ 是函数 是函数 的一个周期”; 的一个周期”; |
D.“ ”是“ ”是“ ”的必要条件. ”的必要条件. |
设 ,且
,且 ,则“函数
,则“函数 在
在 上是减函数”是“函数
上是减函数”是“函数 在
在 上是增函数”的( )
上是增函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“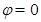 ”是“函数
”是“函数 为奇函数”的( )
为奇函数”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.非充分非必要条件 |
已知函数 ,其中
,其中 为常数.那么“
为常数.那么“ ”是“
”是“ 为奇函数”的( )
为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
条件 ,条件
,条件 ;若p是q的充分而不必要条件,则
;若p是q的充分而不必要条件,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
以下命题中:① 为假命题,则
为假命题,则 与
与 均为假命题
均为假命题
②对具有线性相关的变量 有一组观测数据
有一组观测数据 ,其回归直线方程是
,其回归直线方程是 ,且
,且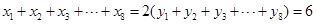 ,则实数
,则实数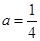
③对于分类变量 与
与 它们的随机变量
它们的随机变量 的观测值
的观测值 来说
来说 越小.“
越小.“ 与
与 有关联”的把握程度越大
有关联”的把握程度越大
④已知 ,则函数
,则函数 的最小值为16. 其中真命题的个数为 ( )
的最小值为16. 其中真命题的个数为 ( )
| A.0 | B.1 | C.2 | D.3 |
使命题“对任意的x∈[1,2],x2-a≤0”为真命题的一个充分不必要条件是( )
| A.a≥4 | B.a≤4 |
| C.a≥5 | D.a≤5 |