题目内容
已知椭圆 的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为
的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F,
,倾斜角为45°的直线l过点F,
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为F1,问抛物线y2=4x上是否存在一点M,使得M与F1关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由。
 的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为
的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F,
,倾斜角为45°的直线l过点F,(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为F1,问抛物线y2=4x上是否存在一点M,使得M与F1关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由。
解:(1)抛物线y2=4x的焦点为F(1,0),准线方程为x=-1,
∴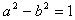 ,①
,①
又椭圆截抛物线的准线x=-1所得弦长为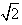 ,
,
∴得上交点为 ,
,
∴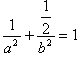 ,②
,②
由①代入②得 (舍去),
(舍去),
从而 ,
,
∴该椭圆的方程为该椭圆的方程为 ;
;
(2)∵倾斜角为45°的直线l过点F,
∴直线l的方程为 ,
,
由(1)知椭圆的另一个焦点为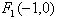 ,
,
设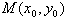 与F1关于直线l对称,
与F1关于直线l对称,
则得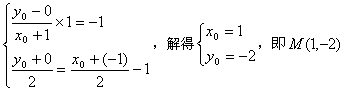 ,
,
又M(1,-2)满足y2=4x,
故点M在抛物线上。
所以抛物线y2=4x上存在一点M(1,-2),使得M与F1关于直线l对称。
∴
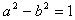 ,①
,①又椭圆截抛物线的准线x=-1所得弦长为
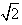 ,
,∴得上交点为
 ,
,∴
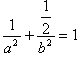 ,②
,②由①代入②得
 (舍去),
(舍去),从而
 ,
,∴该椭圆的方程为该椭圆的方程为
 ;
;(2)∵倾斜角为45°的直线l过点F,
∴直线l的方程为
 ,
,由(1)知椭圆的另一个焦点为
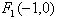 ,
,设
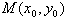 与F1关于直线l对称,
与F1关于直线l对称,则得
 ,
,又M(1,-2)满足y2=4x,
故点M在抛物线上。
所以抛物线y2=4x上存在一点M(1,-2),使得M与F1关于直线l对称。

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
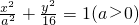 的一个焦点F(3,0),则a=________.
的一个焦点F(3,0),则a=________. 的一个焦点F(3,0),则a= .
的一个焦点F(3,0),则a= . 的一个焦点F(3,0),则a= .
的一个焦点F(3,0),则a= .