题目内容
【题目】已知点F1、F2为双曲线C:x2﹣ ![]() =1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
=1的左、右焦点,过F2作垂直于x轴的直线,在x轴上方交双曲线C于点M,∠MF1F2=30°.
(1)求双曲线C的方程;
(2)过双曲线C上任意一点P作该双曲线两条渐近线的垂线,垂足分别为P1、P2 , 求 ![]() 的值.
的值.
【答案】
(1)解:设F2,M的坐标分别为 ![]() ,
,
因为点M在双曲线C上,所以 ![]() ,即
,即 ![]() ,所以
,所以 ![]() ,
,
在Rt△MF2F1中,∠MF1F2=30°, ![]() ,所以
,所以 ![]()
由双曲线的定义可知: ![]()
故双曲线C的方程为: ![]()
(2)解:由条件可知:两条渐近线分别为 ![]()
设双曲线C上的点Q(x0,y0),设两渐近线的夹角为θ,
则点Q到两条渐近线的距离分别为 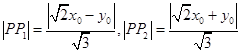 ,
,
因为Q(x0,y0)在双曲线C: ![]() 上,
上,
所以 ![]() ,又cosθ=﹣
,又cosθ=﹣ ![]() ,
,
所以 ![]() =﹣
=﹣ 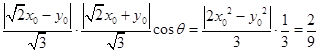
【解析】(1)设F2 , M的坐标分别为 ![]() ,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用双曲线的定义,即可求双曲线C的方程;(2)求出两条渐近线方程,可得点Q到两条渐近线的距离,设两渐近线的夹角为θ,可得
,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用双曲线的定义,即可求双曲线C的方程;(2)求出两条渐近线方程,可得点Q到两条渐近线的距离,设两渐近线的夹角为θ,可得 ![]() ,利用向量的数量积公式,即可求
,利用向量的数量积公式,即可求 ![]() 的值.
的值.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目