题目内容
3.讨论方程4x3+x-15=0在[1,2]内实数解的存在性,并说明理由.分析 令f(x)=4x3+x-15,求导f′(x)=12x2+1>0,从而判断函数的单调性,从而结合零点的判定定理求解即可.
解答 解:令f(x)=4x3+x-15,
则f′(x)=12x2+1>0,
∴f(x)=4x3+x-15在[1,2]上单调递增,
又∵f(1)=4+1-15<0,f(2)=32+2-15<0,
∴f(x)=4x3+x-15在[1,2]上有且只有一个解.
点评 本题考查了导数的综合应用及零点的判定定理的应用.

练习册系列答案
相关题目
11.已知直线l的方程为x=1.则该方程表示( )
| A. | 经过点(1,2)垂直x轴的直线 | B. | 经过点(1,2)垂直y轴的直线 | ||
| C. | 经过点(2,1)垂直x轴的直线 | D. | 经过点(2,1)垂直y轴的直线 |
 把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求: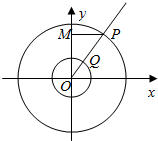 如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.
如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.