题目内容
已知：f（a）=
，
（1）化简f（a）；
（2）若a=
π，求f（a）的值；
（3）若f（a）=
，且
＜a＜
，求cosa-sina的值．
| sin2(π-a)•cos(2π-a)•tan(-π+a) |
| sin(-π+a)tan(3π-a) |
（1）化简f（a）；
（2）若a=
| 5 |
| 4 |
（3）若f（a）=
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
分析：（1）利用诱导公式化简即可得到结果；
（2）将α的值代入计算即可求出值；
（3）根据f（α）=-sinαcosα=
，两边加上1，利用同角三角函数间的基本关系化简，根据α的范围判断cosα-sinα为正数，开方即可求出值．
（2）将α的值代入计算即可求出值；
（3）根据f（α）=-sinαcosα=
| 1 |
| 8 |
解答：解：（1）f（α）=
=-sinαcosα；
（2）将α=
代入得：f（
）=-sin
cos
=-
；
（3）∵f（α）=-sinαcosα=
，
∴1-sinαcosα=（cosα-sinα）2=
，
∵
＜α＜
，∴cosα＞sinα，
则cosα-sinα=
．
| -sin2αcosα•tanα |
| sinαtanα |
（2）将α=
| 5π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
| 5π |
| 4 |
| 1 |
| 2 |
（3）∵f（α）=-sinαcosα=
| 1 |
| 8 |
∴1-sinαcosα=（cosα-sinα）2=
| 9 |
| 8 |
∵
| π |
| 4 |
| π |
| 2 |
则cosα-sinα=
3
| ||
| 4 |
点评：此题考查了运用诱导公式化简求值，以及同角三角函数间的基本关系，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
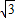sin2ω+2cos2ωx-1（ω＞0）的最小正周期为2π．
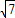，sinB=2sinC，求△ABC的面积S．
sin
ax cos ax＋2 cos2 ax的周期为π，其中a＞0．