题目内容
已知一动圆M,恒过点F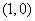 ,且总与直线
,且总与直线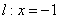 相切.
相切.
(Ⅰ)求动圆圆心M的轨迹C的方程;
(Ⅱ)探究在曲线C上,是否存在异于原点的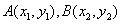 两点,当
两点,当 时,
时,
直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
【答案】
解: (1) 因为动圆M,过点F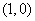 且与直线
且与直线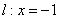 相切,所以圆心M到F的距离等于到直线
相切,所以圆心M到F的距离等于到直线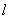 的距离.所以,点M的轨迹是以F为焦点,
的距离.所以,点M的轨迹是以F为焦点, 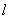 为准线的抛物线,且
为准线的抛物线,且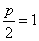 ,
,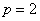 ,
,
所以所求的轨迹方程为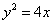 5分
5分
(2) 假设存在A,B在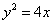 上,
上,
所以,直线AB的方程: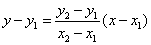 ,即
,即
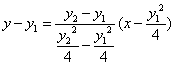 7分
7分
即AB的方程为: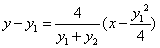 ,即
,即
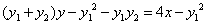
即: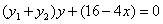 ,
10分
,
10分
令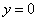 ,得
,得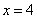 ,
,
所以,无论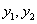 为何值,直线AB过定点(4,0)
12分
为何值,直线AB过定点(4,0)
12分

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 相切,
相切,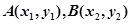 两点,当
两点,当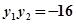 时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.
时,直线AB恒过定点?若存在,求出定点坐标;若不存在,说明理由.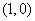 ,且总与直线
,且总与直线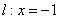 相切.
相切. 两点,当
两点,当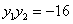 时,
时,