题目内容
已知某公司为上海世博会生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2.7万元,设该公司年内共生产该特许商品x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=
.
(Ⅰ)写出年利润W(万元)关于该特许商品x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
|
(Ⅰ)写出年利润W(万元)关于该特许商品x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
分析:(Ⅰ)当0<x≤10时,W=xR(x)-(10+2.7x)=8.1x-
-10,当x>10时,W=xR(x)-(10+2.7x)=98-
-2.7x,由此能求出年利润W(万元)关于该特许商品x(千件)的函数解析式.
(Ⅱ)当0<x≤10时,由W′=8.1-
=0,得x=9,推导出当x=9时,W取最大值,且wmax=38.6;当x>10时,W≤38.由此得到当年产量为9千件时,该公司在该特许商品生产中获利最大.
| x3 |
| 3 |
| 1000 |
| 3x |
(Ⅱ)当0<x≤10时,由W′=8.1-
| x2 |
| 10 |
解答:解:(Ⅰ)当0<x≤10时,
W=xR(x)-(10+2.7x)=8.1x-
-10,
当x>10时,W=xR(x)-(10+2.7x)=98-
-2.7x,
∴W=
.…(6分)
(Ⅱ)①当0<x≤10时,
由W′=8.1-
=0,得x=9,且当x∈(0,9)时,w′>0,
当x∈(9,10)时,w′<0.
∴当x=9时,W取最大值,且wmax=8.1×9-
×93-10=38.6.…(9分)
②当x>10时,W=98-(
+2.7x)<98-2
=38,
当且仅当
=2.7x,即x=
时,Wmax=38.
综合①、②知x=9时,W取最大值.…(11分)
所以当年产量为9千件时,该公司在该特许商品生产中获利最大.…(12分)
W=xR(x)-(10+2.7x)=8.1x-
| x3 |
| 30 |
当x>10时,W=xR(x)-(10+2.7x)=98-
| 1000 |
| 3x |
∴W=
|
(Ⅱ)①当0<x≤10时,
由W′=8.1-
| x2 |
| 10 |
当x∈(9,10)时,w′<0.
∴当x=9时,W取最大值,且wmax=8.1×9-
| 1 |
| 30 |
②当x>10时,W=98-(
| 1000 |
| 3x |
|
当且仅当
| 1000 |
| 3x |
| 100 |
| 9 |
综合①、②知x=9时,W取最大值.…(11分)
所以当年产量为9千件时,该公司在该特许商品生产中获利最大.…(12分)
点评:本题考查函数的解析式的求法,考查年利润的最大值的求法.解时要认真审题,注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
 (
( )元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值
)元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值 的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格
的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格 表示为价格变化值
表示为价格变化值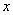 (
(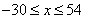 )元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值
)元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值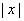 的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格
的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格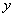 表示为价格变化值
表示为价格变化值