题目内容
为赢得2010年上海世博会的制高点,某公司最近进行了世博特许产品的市场分析,调查显示,该产品每件成本9元,售价为30元,每天能卖出432件,该公司可以根据情况可变化价格x(-30≤x≤54)元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值|x|的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格x成正比,每提价1元则每天少卖8件,且仅在提价销售时每件产品被世博管委会加收1元的管理费.(Ⅰ)试将每天的销售利润y表示为价格变化值x的函数;
(Ⅱ)试问如何定价才能使产品销售利润最大?
【答案】分析:(1)根据“每天多卖出的产品件数与商品单价的降低值|x|的平方成正比”和“商品单价降低2元时,每天多卖出24件”,建立降价多卖产品的模型,再根据销售利润的构成,建立利润函数模型.当提价x时,由“销售减少,减少的件数与提高价格x成正比,每提价1元则每天少卖8件,”,建立少卖产品的模型,再由销售利润的构成建立利润函数模型,构造分段函数.
(2)根据(1)按分段函数求最值来完成,思路是求每一段的最大值,然后从中取最大的作为原函数的最大值.
解答:解:(1)当降价|x|时,则多卖产品kx2,由已知得:24=kx2=4k⇒k=6,
所以f(x)=(30+x-9)(432+6x2)=6(x3+21x2+72x+1512)(3分)
当提价x时,f(x)=(30+x-10)•(432-8x)=-8x2+272x+8640,(2分)
所以 (6分)
(6分)
(2)当降价销售时,
f(x)=6(x3+21x2+72x+1512),
f'(x)=18(x2+14x+24)=18(x+12)(x+2)=0⇒x1=-12,x2=-2,
所以有
即f(x)在x=-12处取得唯一极大值f(-12)=11664,
∴f(x)max=11664,(9分)
当提价销售时,f(x)=-8x2+272x+8640=-8(x2-34x)+8640=-8[(x-17)2]+10952≤10952<11664(11分)
所以当定价18元时,销售额最大.(12分)
点评:本题主要考查函数模型的建立和应用,主要涉及分段函数的求法,导数法,二次函数法求最值及分类讨论思想.
(2)根据(1)按分段函数求最值来完成,思路是求每一段的最大值,然后从中取最大的作为原函数的最大值.
解答:解:(1)当降价|x|时,则多卖产品kx2,由已知得:24=kx2=4k⇒k=6,
所以f(x)=(30+x-9)(432+6x2)=6(x3+21x2+72x+1512)(3分)
当提价x时,f(x)=(30+x-10)•(432-8x)=-8x2+272x+8640,(2分)
所以
 (6分)
(6分)(2)当降价销售时,
f(x)=6(x3+21x2+72x+1512),
f'(x)=18(x2+14x+24)=18(x+12)(x+2)=0⇒x1=-12,x2=-2,
所以有

即f(x)在x=-12处取得唯一极大值f(-12)=11664,
∴f(x)max=11664,(9分)
当提价销售时,f(x)=-8x2+272x+8640=-8(x2-34x)+8640=-8[(x-17)2]+10952≤10952<11664(11分)
所以当定价18元时,销售额最大.(12分)
点评:本题主要考查函数模型的建立和应用,主要涉及分段函数的求法,导数法,二次函数法求最值及分类讨论思想.

练习册系列答案
相关题目
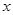 (单位:万元,
(单位:万元,
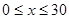 )的平方成正比,已知商品单价降低2万元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2万元时,一星期多卖出24件. (
( )元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值
)元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值 的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格
的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格 表示为价格变化值
表示为价格变化值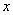 (
(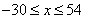 )元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值
)元出售产品;若降低价格,则销售量增加,且每天多卖出的产品件数与商品单价的降低值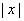 的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格
的平方成正比,已知商品单价降低2元时,每天多卖出24件;若提高价格,则销售减少,减少的件数与提高价格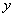 表示为价格变化值
表示为价格变化值