题目内容
已知函数f(x)=x3+ax2+b的图象上的一点P(1,0),且在点P处的切线与直线3x+y=0平行.(1)求函数f(x)的解析式;
(2)求函数f(x)在区间[0,t](0<t<3)上的最大值和最小值.
(3)在(1)的结论下,关于x的方程f(x)=c在区间[1,3]上恰有两个相异的实根,求实数c的取值范围.
思路分析:由导数的几何意义写出过P点的切线方程,结合已知条件求出a,b,利用导数求最值,注意对参数t的讨论.求c的范围要借助函数的单调性,用方程的观点列不等式.
解:(1)因为f′(x)=3x2+2ax,所以曲线在P(1,0)处的切线斜率为f′(1)=3+2a,即3+2a=-3,a=-3.
又函数过(1,0)点,即-2+b=0,b=2.
所以a=-3,b=2,f(x)=x3-3x2+2.
(2)由f(x)=x3-3x2+2,f′(x)=3x2-6x.由f′(x)=0,得x=0或x=2.
①当0<t≤2时,在区间(0,t)上f′(x)<0,f(x)在[0,t]上是减函数,所以f(x)max=f(0)=2,f(x)min=f(t)=t3-3t2+2.
②当2<t<3时,当x变化时,f′(x)、f(x)的变化状态见下表:
x | 0 | (0,2) | 2 | (2,t) | t |
f′(x) | 0 | - | 0 | + | + |
f(x) | 2 | ?↘ | -2 | ?↗ | t3-3t2+2 |
f(x)min=f(2)=-2.
f(x)max为f(0)与f(t)中较大的一个.
f(t)-f(0)=t3-3t2=t2(t-3)<0.
所以f(x)max=f(0)=2.
(3)令g(x)=f(x)-c=x3-3x2+2-c,g′(x)=3x2-6x=3x(x-2).
在x∈[1,2)上,g′(x)<0;在x∈(2,3]上,g′(x)>0.
要使g(x)=0在[1,3]上恰有两个相异的实根,则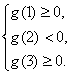

练习册系列答案
相关题目