题目内容
4.设全集是实数集R,A={x|$\frac{1}{2}$≤x≤3},B={x|2a<x<a+2}.(1)当a=-1时,求A∩B和A∪B;
(2)若(∁RA)∩B=B,求实数a的取值范围.
分析 (1)把a=-1代入集合B,求出集合B的解集,再根据交集和并集的定义进行求解;
(2)因为(CRA)∩B=B,可知B⊆CRA,求出CRA,再根据子集的性质进行求解.
解答 解:(1)当a=-1时,B={x|-2<x<1},
则A∩B={x|$\frac{1}{2}$≤x<1},A∪B={x|-2<x≤3}
(2)若(CRA)∩B=B,则B⊆CRA={x|x>3或x<$\frac{1}{2}$},
1°当a≥2时,B=∅,满足B⊆CRA.
2°当a<2时,B⊆CRA,
则a+2≤$\frac{1}{2}$或2a≥3,
∴a≤-$\frac{3}{2}$或a≥$\frac{3}{2}$,
∴a≤-$\frac{3}{2}$或$\frac{3}{2}$≤a<2.
综上,a≤-$\frac{3}{2}$或a≥$\frac{3}{2}$.
点评 本题主要考查交集和并集的定义以及子集的性质,是一道基础题,解题过程中用到了分类讨论的思想.

练习册系列答案
相关题目
13.下列命题中正确的是( )
| A. | 任何一个集合必有两个以上的子集 | B. | 空集是任何集合的子集 | ||
| C. | 空集没有子集 | D. | 空集是任何集合的真子集 |
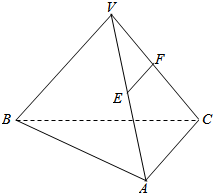 如图,在三棱锥V-ABC中,点E∈VA,点F∈VC,经过EF作一个截面γ,使VB∥平面γ,试作平面γ与三棱锥V-ABC表面的交线.
如图,在三棱锥V-ABC中,点E∈VA,点F∈VC,经过EF作一个截面γ,使VB∥平面γ,试作平面γ与三棱锥V-ABC表面的交线.