题目内容
如图3-4-2,动物园要围成相同的长方形虎笼四间,一面可利用原有的墙,其它各面用钢筋网围成.(1)现有可围36米长的钢筋材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼面积最大?
(2)若使每间虎笼面积为24 m2,则每间虎笼的长、宽各设计为多少时,可使围成四间虎笼的钢筋总长度最小?
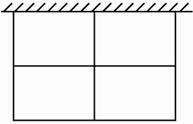
图3-4-2
解:(1)设每间虎笼长为x米,宽为 y米,则由条件知4x+6y=36,即2x+3y=18.
设每间虎笼的面积为S,则S=xy.
方法一:由于2x+3y≥![]() ,
,
∴![]() ≤18,得xy≤
≤18,得xy≤![]() ,即S≤
,即S≤![]() .
.
当且仅当2x=3y时等号成立.
由![]() 解得
解得![]()
故每间虎笼长为4.5 m,宽为3 m时,可使面积最大.
方法二:由2x+3y=18,得x=9-![]() y.
y.
∵x>0,∴0<y<6.
S=xy=(9-![]() y)y=
y)y=![]() (6-y)y.
(6-y)y.
∵0<y<6,∴6-y>0.
∴S≤![]() [
[![]() ]2=
]2=![]() .
.
当且仅当6-y=y,即y=3时,等号成立,此时x =4.5.故每间虎笼长4.5 m,宽3 m时,可使面积最大.
(2)由条件知S=xy=24.
设钢筋网总长为l,则l=4x+6y.
方法一:∵2x+3y≥![]() =24,
=24,
∴l=4x+6y=2(2x+3y)≥48,当且仅当2x=3y时等号成立.
由![]() 解得
解得![]()
故每间虎笼长6 m,宽4 m,可使钢筋网总长最小.
方法二:由xy=24,得x=![]() .
.
∴l=4x+6y=![]() +6y=6(
+6y=6(![]() +y)≥6×
+y)≥6×![]() =48,
=48,
当且仅当![]() =y,即y=4时,等号成立,此时x=6.
=y,即y=4时,等号成立,此时x=6.
故每间虎笼长6 m,宽4 m时,可使钢筋总长最小.

练习册系列答案
相关题目