题目内容
对实数a和b，定义运算“?”：a?b＝
，设函数f(x)＝(x2－2)?(x－x2)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是( )
A．(－∞，－2]∪ | B．(－∞，－2]∪ |
C． ∪ | D．∪ |
B
解析试题分析：由已知得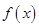
＝
＝
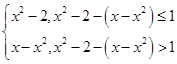
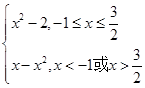
则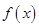的图象如图.
∵
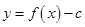的图象与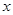
轴恰有两个公共点，
∴
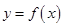与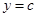
的图象恰有两个公共点，
由图象知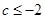
，或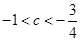
.
考点：分段函数的解析式求法及其图像的作法，数形结合思想.
练习册系列答案
相关题目
当
时，则下列大小关系正确的是 （ ）
A． | B． |
C． | D． |
的定义域为
，若对任意的
，当
时，都有
，则称函数
上为非减函数，且满足以下三个条件：
；②
；③
.则
（ ）
已知函数
，（
且
）是
上的减函数，则
的取值范围是（ ）
A． | B． | C． | D． |
若
，则（ ）
A． < < | B．<< |
| C．<< | D．<< |
，已知函数
，那么
的大致图象是（ ）
函数
是幂函数，且在
上为增函数，则实数
的值是（ ）
A． | B． | C． | D．或 |
，为了保证正常用电，安装后采用太阳能和电能互补供电的模式.假设在此模式下，安装后该企业每年消耗的电费
（单位：万元）与安装的这种太阳能电池板的面积
（单位：平方米）之间的函数关系是
.记该企业安装这种太阳能供电设备的费用与该企业15年共将消耗的电费之和
（万元），则
等于（ ）
已知集合
，
，则
为（ ）
A． | B． | C． | D． |