题目内容
下列有关命题的说法正确的是( )A.命题P:?X∈R,f(X)=cos2x+
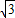 sin2x≤3,则-p:?x∈R,
sin2x≤3,则-p:?x∈R,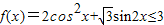 ,且原命题p是真命题
,且原命题p是真命题B.命题“若x=y,则sinx=siny”的逆否命题为假命题
C.已知
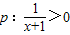 ,则
,则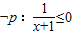
D.在△ABC中,角A,B,C的对边分别是a,b,c,则a<b?cos2A>cos2B
【答案】分析:A,由全称命题得到存在性命题,要注意形式;B,原命题与逆否命题同真假;C,对命题的否定存在问题;
D,由正弦定理可以把边的关系转化为正弦的关系,再利用同角三角函数关系转化为余弦的关系.
解答:解:A: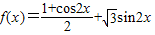 =
=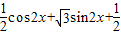 =
=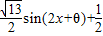 (其中θ由
(其中θ由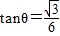 确定),∴?X∈R,f(x)
确定),∴?X∈R,f(x)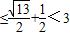 ;对其否定为:?x∈R,
;对其否定为:?x∈R,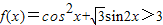 ,故该选项不正确;
,故该选项不正确;
B:命题“若x=y,则sinx=siny”的逆否命题与原命题真假一致,而原命题为真,故逆否命题为真,故该选项不正确;
C:-p:?x∈R,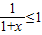 ,故该选项不正确;
,故该选项不正确;
D:△ABC中,由正弦定理有
a>b?sinA>sinB?sin2A>sin2B?1-cos2A>1-cos2B
∴cos2A<cos2B,故该选项正确.
故选D.
点评:本题主要考查了命题、四种命题之间关系及真假的判断、全称命题、存在性命题,三角函数的有关知识,是一道综合性较强的题目.
D,由正弦定理可以把边的关系转化为正弦的关系,再利用同角三角函数关系转化为余弦的关系.
解答:解:A:
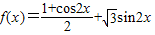 =
=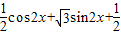 =
=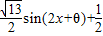 (其中θ由
(其中θ由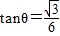 确定),∴?X∈R,f(x)
确定),∴?X∈R,f(x)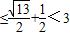 ;对其否定为:?x∈R,
;对其否定为:?x∈R,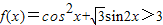 ,故该选项不正确;
,故该选项不正确;B:命题“若x=y,则sinx=siny”的逆否命题与原命题真假一致,而原命题为真,故逆否命题为真,故该选项不正确;
C:-p:?x∈R,
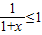 ,故该选项不正确;
,故该选项不正确;D:△ABC中,由正弦定理有
a>b?sinA>sinB?sin2A>sin2B?1-cos2A>1-cos2B
∴cos2A<cos2B,故该选项正确.
故选D.
点评:本题主要考查了命题、四种命题之间关系及真假的判断、全称命题、存在性命题,三角函数的有关知识,是一道综合性较强的题目.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目