题目内容
设已知点 .
.(Ⅰ)若
 ,求角α的值;
,求角α的值;(Ⅱ)若
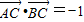 ,求
,求 的值.
的值.
【答案】分析:(Ⅰ)解法一,依题意,由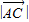 =
=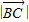 ,可求得cosα=sinα,结合题意可求得角α的值;
,可求得cosα=sinα,结合题意可求得角α的值;
解法二,由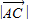 =
=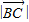 ,可知点C在直线y=x上,而α∈(
,可知点C在直线y=x上,而α∈(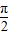 ,
,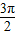 ),可求得角α的值;
),可求得角α的值;
(Ⅱ)由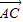 •
•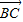 =-1,可求得sinα+cosα=
=-1,可求得sinα+cosα= ,将所求关系式切化弦后得
,将所求关系式切化弦后得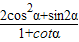 =2sinαcosα,利用(sinα+cosα)2=1+2sinαcosα即可求得答案.
=2sinαcosα,利用(sinα+cosα)2=1+2sinαcosα即可求得答案.
解答:解:(Ⅰ)解法一:∵A(3,0)、B(0,3)、C(cosα,sinα),
∴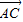 =(cosα-3,sinα),
=(cosα-3,sinα),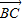 =(cosα,sinα-3). …(2分)
=(cosα,sinα-3). …(2分)
由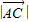 =
=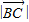 ,得
,得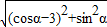 =
=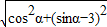 .
.
即cosα=sinα. …(4分)
∵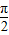 <α<
<α<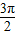 ,
,
∴α=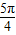 .…(6分)
.…(6分)
解法二:∵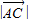 =
=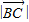 ,
,
∴点C在直线y=x上.…(3分)
则sinα=cosα. …(4分)
∵α∈(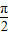 ,
,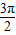 ),
),
∴α=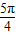 .…(6分)
.…(6分)
(Ⅱ)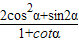 =
=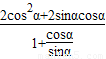
=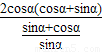 =2sinαcosα.…(8分)
=2sinαcosα.…(8分)
由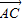 •
•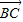 =-1,得(cosα-3)cosα+sinα(sinα-3)=-1.…(10分)
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.…(10分)
即 sinα+cosα= .
.
∴(sinα+cosα)2=1+2sinαcosα= ,即2sinαcosα=-
,即2sinαcosα=- . …(12分)
. …(12分)
∴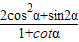 =
=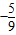 .…(13分)
.…(13分)
点评:本题考查三角函数的恒等变换及化简求值,考查平面向量数量积的坐标运算,考查综合分析与运算的能力,属于中档题.
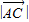 =
=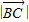 ,可求得cosα=sinα,结合题意可求得角α的值;
,可求得cosα=sinα,结合题意可求得角α的值;解法二,由
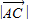 =
=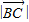 ,可知点C在直线y=x上,而α∈(
,可知点C在直线y=x上,而α∈(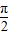 ,
,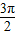 ),可求得角α的值;
),可求得角α的值;(Ⅱ)由
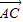 •
•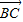 =-1,可求得sinα+cosα=
=-1,可求得sinα+cosα= ,将所求关系式切化弦后得
,将所求关系式切化弦后得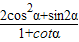 =2sinαcosα,利用(sinα+cosα)2=1+2sinαcosα即可求得答案.
=2sinαcosα,利用(sinα+cosα)2=1+2sinαcosα即可求得答案.解答:解:(Ⅰ)解法一:∵A(3,0)、B(0,3)、C(cosα,sinα),
∴
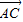 =(cosα-3,sinα),
=(cosα-3,sinα),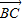 =(cosα,sinα-3). …(2分)
=(cosα,sinα-3). …(2分)由
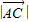 =
=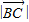 ,得
,得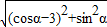 =
=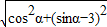 .
.即cosα=sinα. …(4分)
∵
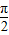 <α<
<α<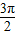 ,
,∴α=
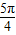 .…(6分)
.…(6分)解法二:∵
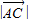 =
=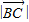 ,
,∴点C在直线y=x上.…(3分)
则sinα=cosα. …(4分)
∵α∈(
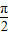 ,
,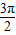 ),
),∴α=
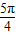 .…(6分)
.…(6分)(Ⅱ)
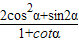 =
=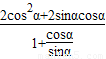
=
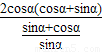 =2sinαcosα.…(8分)
=2sinαcosα.…(8分)由
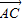 •
•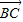 =-1,得(cosα-3)cosα+sinα(sinα-3)=-1.…(10分)
=-1,得(cosα-3)cosα+sinα(sinα-3)=-1.…(10分)即 sinα+cosα=
 .
.∴(sinα+cosα)2=1+2sinαcosα=
 ,即2sinαcosα=-
,即2sinαcosα=- . …(12分)
. …(12分)∴
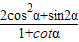 =
=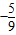 .…(13分)
.…(13分)点评:本题考查三角函数的恒等变换及化简求值,考查平面向量数量积的坐标运算,考查综合分析与运算的能力,属于中档题.

练习册系列答案
相关题目
 及圆
及圆 :
: .
. 过点
过点 且与圆心
且与圆心 与圆
与圆 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆 的方程;
的方程; (3)设直线
(3)设直线 与圆
与圆 ,
, 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点 垂直平分弦
垂直平分弦 ?若存在,求出实数
?若存在,求出实数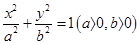 的离心率
的离心率 ,连接椭圆的四个顶点得到的菱形的
,连接椭圆的四个顶点得到的菱形的
 若
若 ;求直线L的倾斜角
;求直线L的倾斜角 若点
若点 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且 ,求
,求 的值
的值 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。 与
与 交点的轨迹
交点的轨迹 的方程式;
的方程式; 与曲线
与曲线 ,已知点
,已知点 的坐标为
的坐标为 ,若点
,若点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 .求
.求 的值.
的值.